Многократное измерение. Анализ априорной информации

Многократное измерение

Исходные данные

Массив экспериментальных данных

14,43; 14,45; 14,43; 14,53; 14,50; 14,46; 14,49; 14,49; 14,54; 14,50;

14,45; 14,53; 14,44; 14,46; 14,55; 14,44; 14,43; 14,48; 14,55; 14,53;

14,55; 14,50; 14,47; 14,44; 14,46; 14,51; 14,53; 14,48; 14,43; 14,48;

14,49; 14,54; 14,53; 14,51; 14,49; 14,46; 15,74; 14,48; 14,47; 14,48;

14,43; 14,44; 14,44; 14,48; 14,54; 14,48; 14,45; 14,51; 14,44; 14,50;

Поправка

Из анализа априорной информации видно, что  поправка измерительного прибора при измерении значения напряжения 10 В  составляет (-0,05 В), а при измерении значения напряжения 15  В  составляет (-0,12 В).

Неисключенная систематическая погрешность результата измерения образуется из неисключенных основной и дополнительной систематических погрешностей средства измерений, которые соответственно равны θ₁=0,2 В и θ₂=0,1 В.

Исключение известных систематических погрешностей

Решив систему из двух уравнений,  рассчитаем коэффициенты а= - 0,014  и  b= 0,09.  Аналитическая зависимость поправки от значения измеряемого значения напряжения имеет вид:

Номер наблюдения, показание измерительного прибора, поправка к показанию в точках наблюдения, а также исправленные результаты наблюдений измеряемого напряжения сведены в табл.2.

Таблица 2

Исправленные результаты наблюдений свести во 2-й и 3-й столбцы табл.3.

Произвести обработку экспериментальных данных, последовательно выполняя расчеты и заполняя 4, 5 и 6 столбцы:

1) рассчитать среднее арифметическое значение;

2) оценку среднеквадратического значения наблюдения;

3)проверить массив экспериментальных данных на наличие ошибок, используя правило “трех сигм“;

4)построить гистограмму;

5)оценить стандартное отклонение среднего арифметического;

6)определить границы случайной и неисключенной систематической погрешностей;

7)определить границы погрешности результата измерения;

8)оформить результата измерения (определить границы, в пределах которых, находится значение измеряемого напряжения переменного тока  мВ, Р=0,95.

Таблица 3

Значения измеренной величины в 14 строчке по правилу 3 сигм принимаем как ошибку, т.к. || - 3S_x > 0. Проведем расчеты повторно и представим результаты в табл. 4.

Таблица 4

После повторного расчета ошибок нет.

Считаем, что результат наблюдения подчиняется нормальному закону распределения вероятности.

Выводы

При равномерном  распределении  НСП границы, в пределах которых находится значение измеряемого напряжения переменного тока,  без учета знака вычисляют по формуле

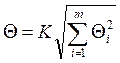= , где   Ɵ_i – граница i-ой неисключенной систематической погрешности;

m - количество неисключенных составляющих;

K – коэффициент, определяемый принятой доверительной вероятностью (К=1,1 при Р=0,95).

Доверительная вероятность для вычисления границ НСП та же, что и при вычислении доверительных границ случайной погрешности результата измерения.

Вычислить доверительные границы погрешности результата измерения.

Если отношение НСП к СКО результата измерения Ɵ/S_xn<0,8, то НСП пренебрегают и принимают, что граница погрешности результата измерения ∆=ɛ. Если Ɵ/Sx_n>8, то пренебрегают случайной погрешностью и принимают, что граница погрешности результата ∆=Ɵ. Т.к. в нашем случае Ɵ/Sx_n = 6,23, то примем, что граница погрешности результата измерения вычисляется по формуле:

, где K – коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешностей;

S_∑ - оценка суммарного СКО результата измерения.

Коэффициент К вычисляют по формуле:

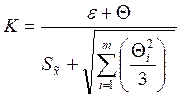, где:

.

При доверительной вероятности Р = 0,95, по таблице функций Лапласа значение t = 1,96. Тогда:

ε = 1,96·0,0181 = 0,03548;

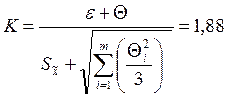
Суммарное  СКО результата измерения оценивают по формуле: