











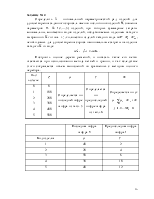
Разделим третью строку на ключевой элемент, равный 5, получим третью строку новой таблицы.
Базисным столбцам соответствуют единичные столбцы.
Расчет остальных значений таблицы:
«БП – Базисный План»:
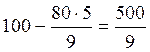 ;
; 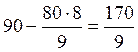 ;
;
«х1»: 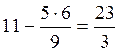 ;
; 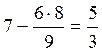 ;
;
«х5»: 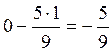 ;
; 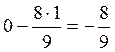 .
.
|
Шаг 1 |
4 |
6 |
0 |
0 |
0 |
||
|
Базис |
БП |
x 1 |
x 2 |
x 3 |
x 4 |
x 5 |
|
|
0 |
x3 |
500/9 |
23/3 |
0 |
1 |
0 |
-5/9 |
|
0 |
x4 |
170/9 |
5/3 |
0 |
0 |
1 |
-8/9 |
|
6 |
x2 |
80/9 |
2/3 |
1 |
0 |
0 |
1/9 |
|
ИС |
160/3 |
0 |
0 |
0 |
0 |
2/3 |
Значения индексной строки
неотрицательны, следовательно получаем оптимальное решение: ![]() ,
, ![]() ;
; 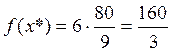 .
.
Ответ: максимальную прибыль от реализации изготовленной продукции, равную 160/3 ед., обеспечивает выпуск только продукции второго типа в количестве 80/9 единиц.
Дана задача нелинейного программирования. Найти максимум и минимум целевой функции графоаналитическим методом. Составить функцию Лагранжа и показать, что в точках экстремума выполняются достаточные условия минимума (максимума).
Т.к. последняя цифра шифра равна 8, то А=2; В=5.
Т.к. предпоследняя цифра шифра равна 1, то следует выбрать задачу № 1.
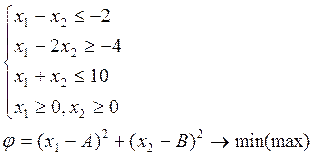
Решение:
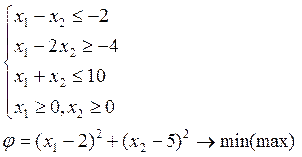
1) Начертим область, которую задает система неравенств.
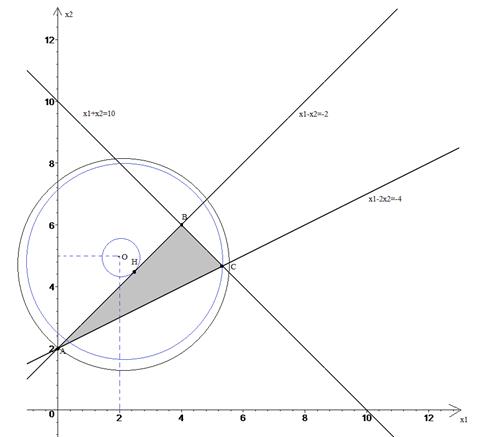
Эта область – треугольник АВС с координатами вершин: А(0; 2); В(4; 6) и С(16/3; 14/3).
Уровни целевой функции ![]() представляют собой окружности с центром в
точке (2; 5). Квадраты радиусов будут являться значениями целевой функции.
Тогда по рисунку видно, что минимальное значение целевой функции достигается в
точке Н, максимальное – либо в точке А, либо в точке С.
представляют собой окружности с центром в
точке (2; 5). Квадраты радиусов будут являться значениями целевой функции.
Тогда по рисунку видно, что минимальное значение целевой функции достигается в
точке Н, максимальное – либо в точке А, либо в точке С.
Значение целевой функции
в точке А: ![]() ;
;
Значение целевой функции
в точке С: 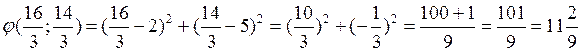 ;
;
Значит, наибольшее значение функции достигается в точке А(0; 2) и равно 13.
Найдем координаты точки Н.
Для этого рассмотрим систему:
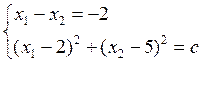 ó
ó
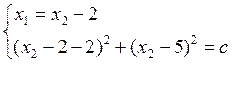
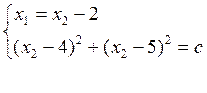 ó
ó 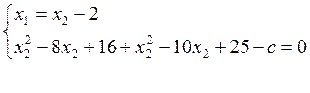
![]()
Прямая ![]() является касательной к окружности, если
уравнение имеет единственное решение. Квадратное уравнение имеет единственное
решение, если дискриминант равен 0.
является касательной к окружности, если
уравнение имеет единственное решение. Квадратное уравнение имеет единственное
решение, если дискриминант равен 0.
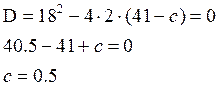
Тогда 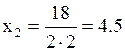 ;
; ![]() ;
; ![]() - минимальное значение функции.
- минимальное значение функции.
2) Составим функцию Лагранжа для нахождение минимального решения:
![]()
Достаточные условия экстремума:
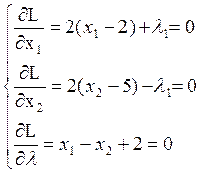
При x1=2.5; x2=4.5 получим:
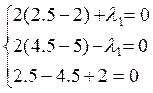 ó
ó 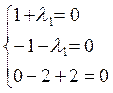
Система имеет решение при
![]() , т.е. достаточные условия экстремума
выполняются.
, т.е. достаточные условия экстремума
выполняются.
Составим функцию Лагранжа для нахождение максимального решения:
![]()
Достаточные условия экстремума:
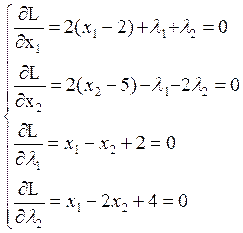
При x1=0; x2=2 получим:
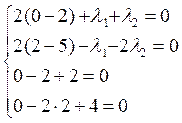 ó
ó 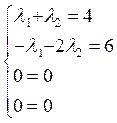 ó
ó 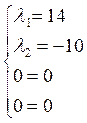
Система также имеет решение, т.е. достаточные условия экстремума выполняются.
Ответ: минимум целевой функции достигается
при ![]() ;
; ![]() ; максимум
целевой функции достигается при
; максимум
целевой функции достигается при ![]() ;
; ![]() .
.
Двум предприятиям выделяются средства в количестве dединиц. При выделении первому предприятию на год xединиц средств оно обеспечивает доход k1xединиц, а при выделении второму предприятию yединиц средств, оно обеспечивает доход k1yединиц. Остаток средств к концу года для первого предприятия равен nx, а для второго my. Как распределить все средства в течение 4-х лет, чтобы общий доход был наибольшим? Задачу решить методом динамического программирования.
i=8, k=1.
A=2200; k1=6; k2=1; n=0.2; m=0.5.
Решение:
Весь период длительностью 4 года разбиваем на 4 этапа, каждый из которых равен одному году. Пронумеруем этапы начиная с первого года. Пусть Хk и Yk – средства, выделенные соответственно предприятиям А и В на k – том этапе. Тогда сумма Хk + Yk =аk является общим количеством средств, используемых на k – том этапе и оставшиеся от предыдущего этапа k – 1. на первом этапе используются все выделенные средства и а1 =2200 ед. доход, который будет получен на k – том этапе, при выделении Хk и Yk единиц составит 6Хk + 1Yk. пусть максимальный доход, полученный на последних этапах начиная с k – того этапа составляет fk (аk) ед. запишем функциональное уравнение Беллмана, выражающее принцип оптимальности: каково бы не было начальное состояние и начальное решение последующее решение должно быть оптимальным по отношению к состоянию, получаемому в результате начального состояния:
![]()
Для каждого этапа нужно выбрать значение Хk, а значение Yk =аk – хk. С учетом этого найдем доход на k – том этапе:
![]()
![]()
Функциональное уравнение Беллмана будет иметь вид:
![]()
Рассмотрим все этапы, начиная с последнего.
При k=4.
![]()
(т.к.
максимум линейной функции ![]() достигается в конце
отрезка [0; а4] при х4 = а4);
достигается в конце
отрезка [0; а4] при х4 = а4);
![]()
![]()
При k=3.
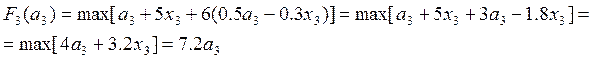
(т.к.
максимум линейной функции ![]() достигается в конце отрезка
[0; а3] при х3 = а3)
достигается в конце отрезка
[0; а3] при х3 = а3)
![]()
![]()
При k=2.
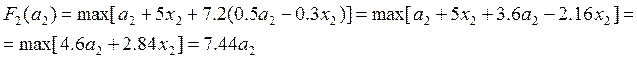
(т.к.
максимум линейной функции ![]() достигается в конце отрезка
[0; а2] при х2 = а2)
достигается в конце отрезка
[0; а2] при х2 = а2)
![]()
![]()
При k=1.
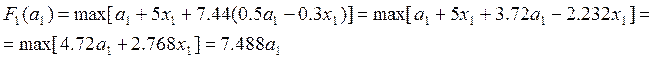
(т.к.
максимум линейной функции ![]() достигается в конце отрезка
[0; а1] при х1 = а1). y1= а1 – х1=0.
достигается в конце отрезка
[0; а1] при х1 = а1). y1= а1 – х1=0.
Таким образом, максимальный доход за 4-е года составит
![]() ед.
ед.
Для получения этого дохода нужно во все четыре года все средства вложить в предприятие А (а1= х1, y1= 0; а2= х2, y2= 0; а3= х3, y3= 0; а4= х4, y4= 0).
Ответ: средства следует вкладывать только в предприятие А суммарный доход за 4 года составит 16473,6 ед.
Определить ![]() - оптимальный параметрический ряд изделий
для удовлетворения заданного спроса, а именно число типов изделий N, значения параметров
- оптимальный параметрический ряд изделий
для удовлетворения заданного спроса, а именно число типов изделий N, значения параметров ![]() (k=1,2,…,5) изделий, при которых суммарные затраты минимальны, множество
видов изделий, обслуживаемых изделием каждого выбранного K-го типа -
(k=1,2,…,5) изделий, при которых суммарные затраты минимальны, множество
видов изделий, обслуживаемых изделием каждого выбранного K-го типа -![]() , количество
изделий каждого вида
, количество
изделий каждого вида ![]() , необходимых для удовлетворения
спроса и минимальные затраты на изделия каждого K-го вида:
, необходимых для удовлетворения
спроса и минимальные затраты на изделия каждого K-го вида:
![]() .
.
Построить полное дерево решений, и показать какие его ветви отсекаются при использовании метода ветвей и границ, и как вследствие этого сокращается объем вычислений по сравнению с методом полного
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.