Рис.5.1. Схема набора модели второй канонической формы.
График переходного процесса представлен на рис.5.2.
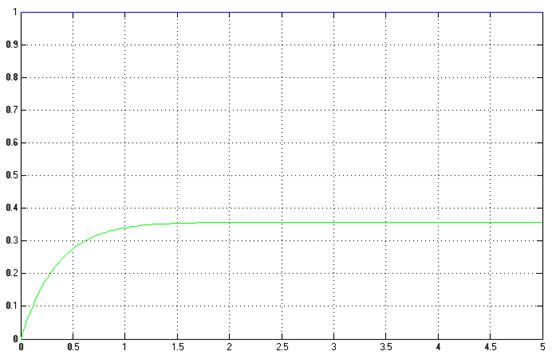
Рис.5.2. График переходной характеристики модели.
Для моделирования весовой характеристики с использованием модели второй канонической формы уберем входное воздействие и установим начальные значения для интеграторов.
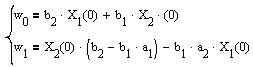
Решив систему, получим:
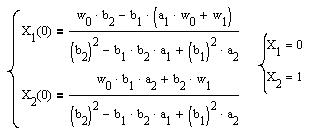
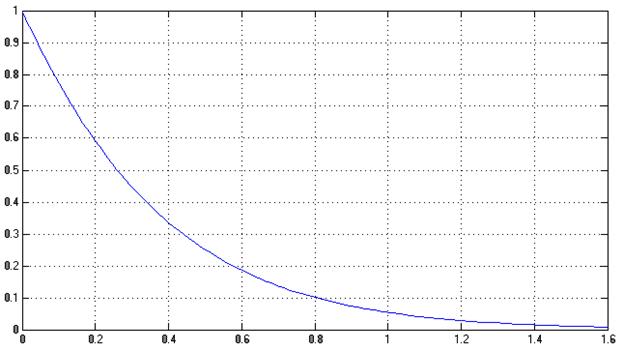
Рис.5.3. График весовой функции модели второй канонической формы.
6. Составление диагональной формы модели системы.
Система уравнений состояния диагональной формы имеет вид:
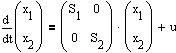
Коэффициенты усилителей в обратных связях интеграторов находим как корни характеристического уравнения системы.
Коэффициенты С1 и С2 вычисляются, исходя из формулы:
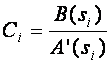, i=1(1)n,
Получаем С1 = -2 и С2 = 4/3. Структура модели диагональной формы представлена на рис.6.1.
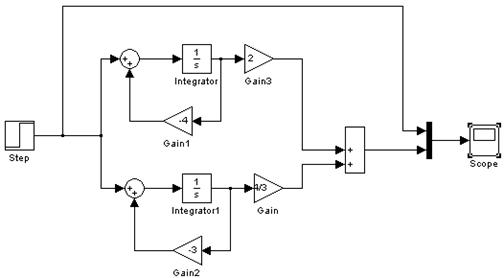
Рис.6.1. Схема набора модели системы.
Рис.6.2. График переходной характеристики модели диагональной формы.
Для моделирования весовой характеристики с использованием модели второй канонической формы уберем входное воздействие и установим начальные значения для интеграторов.
Начальные значения найдем из системы:
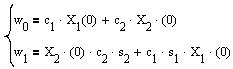
Откуда:
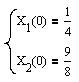
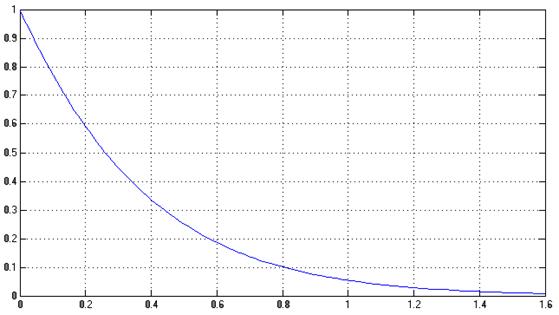
Рис.6.3. График весовой функции модели диагональной формы.
7. Вычислим явные аналитические выражения весовой и переходной функции.
Если корни характеристического уравнения системы различны, то весовая функция определяется соотношением:
,
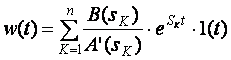где
1(t) – единичная функция;
sk , k = 1(1)n – корни характеристического уравнения;
Переходная функция определяется выражением
,
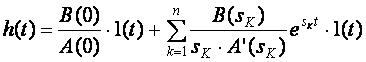Корни характеристического уравнения:
Тогда уравнение весовой функции:
График весовой функции представлен на рис.7.1.
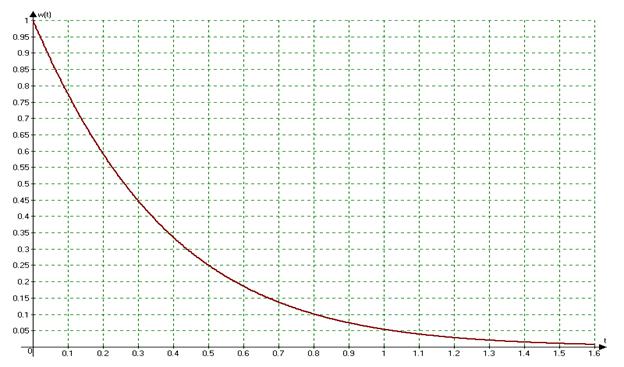
Рис.7.1. График весовой функции исследуемой системы.
Уравнение переходной характеристики:
График переходной характеристики системы представлен на рис.7.2.
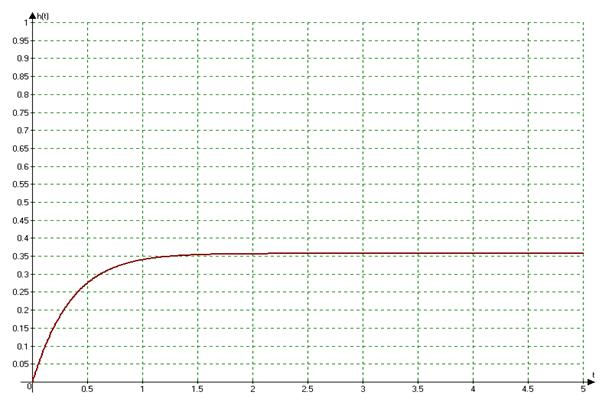
Рис.7.2. График переходной характеристики исследуемой системы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.