Поляризация диэлектриков. Общие сведения об электрических свойствах диэлектриков (характеристики диэлектриков)

Поверхностной плотностью заряда называется отношение заряда к площади заряженной поверхности. Единица СИ поверхностной плотности заряда                                            

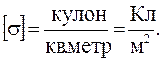
Если s - поверхностная плотность заряда, Q – заряд поверхности проводника, S – площадь поверхности проводника, то

СИ s Q S Кл/м2 Кл м2

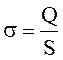.                                                                                                 (2.7)

Наличие зарядов приводит к возникновению сил, которые в свою очередь действуют на заряды, помещенные в электрическое поле. Причина и следствие здесь взаимно переплетаются.

СИ s e0 Е Кл/м2 Кл/(В×м) В/м

Если s - поверхностная плотность заряда, Е – напряженность электрического поля, e₀=8,85×10^-12 Кл/(В×м) – электрическая постоянная, то

.                                                                                          (2.8)

С помощью формулы (2.6) можно определить только величину, но не направление электрического поля. Так как силовые линии перпендикулярны поверхности проводника, для определения направления поля надо построить нормаль к поверхности.

2.4. Определение степени поляризации Закон Кулона, точечные заряды

Под электрическим полем понимают особое состояние пространства, обусловленное присутствием в нем заряда. Электрическое поле какого-нибудь заряда может быть обнаружено по силе, с которой это поле действует на другой заряд. Сила взаимодействия двух зарядов зависит от величины зарядов, от расстояния между ними и от свойств среды, их разделяющей. Эта зависимость носит название закона Кулона.

Для диэлектрической среды, отличающейся от вакуума, сила взаимодействия зарядов определяется по формуле:

			(2.9)

 

                       где F - сила взаимодействия двух точечных зарядов; Q₁ – величина одного точечного заряда; Q₂ – величина другого точечного заряда;  r – расстояние между зарядами; e_а=e₀e_r – абсолютная диэлектрическая проницаемость; e₀=8,85×10^-12 Ф/м – электрическая постоянная; e_r – относительная диэлектрическая проницаемость, (см. табл. 2.1); т.е. сила взаимодействия зарядов описывается законом Кулона.

Обратите внимание: формула с хорошей точностью справедлива и в случае заряженных шаров, если расстояние между ними велико по сравнению с радиусами. В этом случае r – расстояние между центрами шаров. 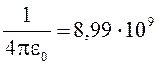                                    м/Ф.

Выражение для напряженности электрического поля, Е, В/м (т.е. отталкивающего усилия, действующего на единичный положительный заряд), создаваемой точечным зарядом q на расстоянии d от него,

CИ Е q d В/м Кл м

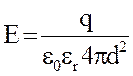.                                                                                     (2.10.)

Энергия электрического поля

В электрическом поле всегда запасена энергия. Она соответствует работе, затрачиваемой на создание поля (на разделение зарядов), и вновь превращается в работу, когда поле исчезает.

Предположим, что в процессе зарядки ток I остается постоянным, а мгновенное напряжение u(t) линейно зависит от времени. Предположим далее, что напряжение в процессе зарядки увеличивается от 0 до U. Тогда если W – энергия заряженного конденсатора; С – емкость конденсатора; U – напряжение между пластинами конденсатора, то энергия заряженного конденсатора определяется выражением

,

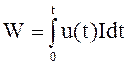или окончательно

.

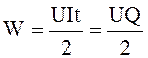Так как согласно формуле 2.10, Q=CU, имеем

CИ W C U Q Дж Ф В Кл

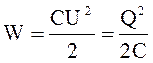.                                                                        (2.11)

Обратите внимание: выражение (2.11) справедливо для электрического поля любой конфигурации.

Полагая в формуле 2.11 С=e_аS/d и U=Ed, получаем для плоского конденсатора

СИ W eа Е S d Дж Кл/(В×м) В/м м2 м

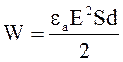.                                                                             (2.12)

CИ W eа D Е V Дж Кл/(В×м) Кл/м2 В/м м3

В случае однородного электрического поля, учитывая, что Sd=V – объем поля и e_аЕ=D, можно написать

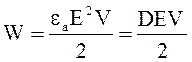.                                                                           (2.13)

2.5. Электрическое смещение Теорема Гаусса

Согласно этой теореме поток вектора электрического смещения D через произвольную замкнутую поверхность равен суммарной величине заряда, расположенного внутри этой поверхности. Если обозначить заряды, заключенные внутри замкнутой поверхности, через Q₁, Q₂, Q₃, ..., Q_n (Q может быть положительным или отрицательным), то теорему Гаусса математически можно выразить через поверхностный интеграл следующим образом:

CИ D dS Ф Кл/м2 м2 Вd

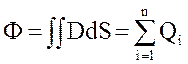.                                                                  (2.14)

Здесь D представляет вектор электрического смещения, dS – вектор, нормальный к элементу поверхности и направленный от нее.

Интегрирование производиться по всей замкнутой поверхности