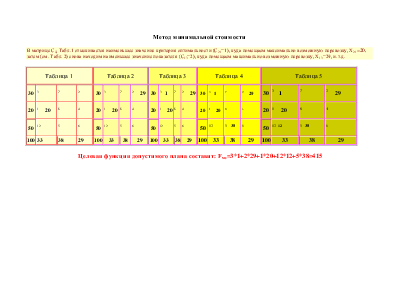
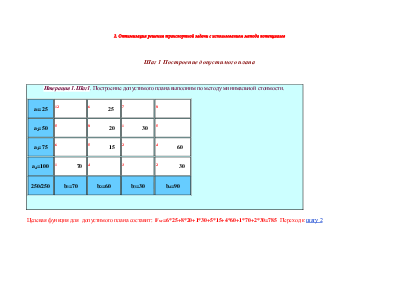



Метод минимальной стоимости
В матрице Cij Табл.1 отыскивается наименьшее значение критерия оптимальности (С21=1), куда помещаем максимально возможную перевозку, Х21=20, затем (см. Табл. 2) снова находим наименьшее значение показателя (С13=2), куда помещаем максимально возможную перевозку, Х13=29, и.т.д.
|
Таблица 1 |
Таблица 2 |
Таблица 3 |
Таблица 4 |
Таблица 5 |
|||||||||||||||
|
30 |
3 |
7 |
2 |
30 |
3 |
7 |
2 29 |
30 |
3 1 |
7 |
2 29 |
30 |
3 1 |
7 |
2 29 |
30 |
3 1 |
7 |
2 29 |
|
20 |
1 20 |
8 |
4 |
20 |
1 20 |
8 |
4 |
20 |
1 20 |
8 |
4 |
20 |
1 20 |
8 |
4 |
20 |
1 20 |
8 |
4 |
|
50 |
12 |
5 |
6 |
50 |
12 |
5 |
6 |
50 |
12 |
5 |
6 |
50 |
12 |
5 38 |
6 |
50 |
12 12 |
5 38 |
6 |
|
100 |
33 |
38 |
29 |
100 |
33 |
38 |
29 |
100 |
33 |
38 |
29 |
100 |
33 |
38 |
29 |
100 |
33 |
38 |
29 |
Целевая функция допустимого плана составит: Fмс=3*1+2*29+1*20+12*12+5*38=415
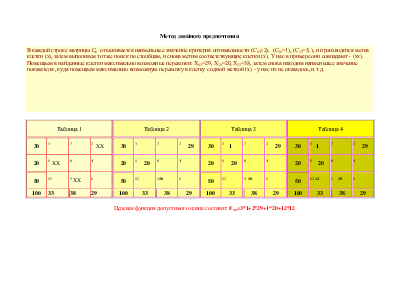
Метод двойного предпочтения
В каждой строке матрицы Cij отыскивается наименьшее значение критерия оптимальности (С13=2), (С21=1), (С32=5, ), и производится метка клетки (х), затем выполняем тот же поиск по столбцам, и снова метим соответствующие клетки (х). У нас в примере они совпадают - (хх). Помещаем в найденные клетки максимально возможные перевозки: Х13=29, Х21=20, Х32=38, затем снова находим наименьшее значение показателя , куда помещаем максимально возможную перевозку в клетку с одной меткой (х) - у нас их не оказалось, и.т.д.
|
Таблица 1 |
Таблица 2 |
Таблица 3 |
Таблица 4 |
||||||||||||
|
30 |
3 |
7 |
2 XX |
30 |
3 |
7 |
2 29 |
30 |
3 1 |
7 |
2 29 |
30 |
3 1 |
7 |
2 29 |
|
20 |
1 XX |
8 |
4 |
20 |
1 20 |
8 |
4 |
20 |
1 20 |
8 |
4 |
20 |
1 20 |
8 |
4 |
|
50 |
12 |
5 XX |
6 |
50 |
12 |
538 |
6 |
50 |
12 |
5 38 |
6 |
50 |
12 12 |
5 38 |
6 |
|
100 |
33 |
38 |
29 |
100 |
33 |
38 |
29 |
100 |
33 |
38 |
29 |
100 |
33 |
38 |
29 |
Целевая функция допустимого плана составит: Fxx=3*1+2*29+1*20+12*12
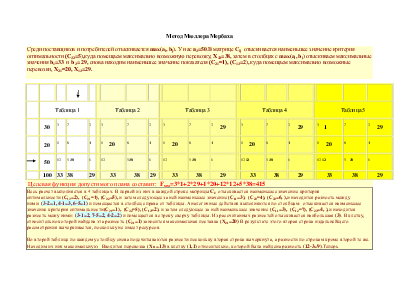
Метод Мюллера Мербаха
Среди поставщиков и потребителей отыскивается max(ai, bj). У нас а3=50.В матрице Cij отыскивается наименьшее значение критерия оптимальности (С32=5),куда помещаем максимально возможную перевозку, Х32=38, затем в столбцах с max(ai, bj) отыскиваем максимальные значения b1=33 и b3= 29, снова находим наименьшее значение показателя (С21=1), (С13=2), куда помещаем максимально возможные перевозки, Х21=20, Х13=29.
|
|
||||||||||||||||||||
|
Таблица 1 |
Таблица 2 |
Таблица 3 |
Таблица 4 |
Таблица 5 |
||||||||||||||||
|
30 |
3 |
7 |
2 |
3 |
7 |
2 |
3 |
7 |
2 29 |
3 |
7 |
2 29 |
3 1 |
7 |
2 29 |
|||||
|
20 |
1 |
8 |
4 |
1 20 |
8 |
4 |
1 20 |
8 |
4 |
1 20 |
8 |
4 |
1 20 |
8 |
4 |
|||||
|
|
50 |
12 |
5 38 |
6 |
12 |
5 38 |
6 |
12 |
5 38 |
6 |
12 12 |
5 38 |
6 |
12 12 |
5 38 |
6 |
||||
|
100 |
33 |
38 |
29 |
33 |
38 |
29 |
33 |
38 |
29 |
33 |
38 |
29 |
33 |
38 |
29 |
|||||
Целевая функция допустимого плана составит: Fмм=3*1+2*29+1*20+12*12+5*38=415
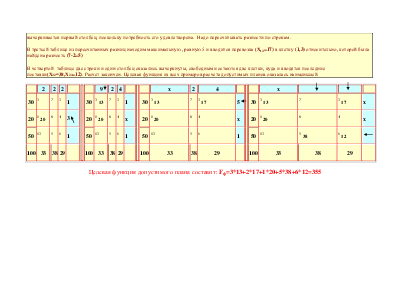
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.