Наиболее существенным показателем для оценки каждого уравнения является коэффициент парного корреляционного отношения, который отображает тесноту связи между результативным показателям и факторным признаком .
Парное корреляционное отношение
рассчитывают по формуле:
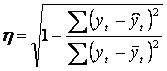
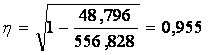
Значение коэффициента парного корреляционного отношения свидетельствует о сильной связи между функцией и аргументом.
Кроме тесноты связи для оценки адекватности уравнения реальным процессам служат следующие показатели:
Средняя ошибка аппроксимации:
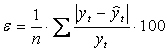
![]()
![]()
Среднее квадратичное отклонение между фактическим и расчетным значением функции:
а)абсолютное
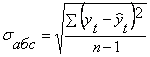
![]()
б)относительное
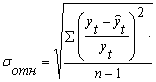
![]()
Среднее отклонение между фактическим и расчетными значениями функций:
а) абсолютное
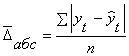
![]()
б) относительное
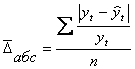
![]()
Построенный на основе начальных данных часовой тренд позволяет составить прогноз на период n+p (p=1,2,3..)
![]()
![]()
Для адекватного прогнозирования не обходимо построить интервальный прогноз, который учитывал бы отклонения от теоретического уровня, которые обусловлены случайными факторами. В интервальном прогнозировании используются интервальные значения прогноза в виде «Вилки» - максимальная и минимальная величина. Доверительные интервалы прогноза могут быть записаны следующим образом:
![]() Ta=2,78
Ta=2,78
![]()
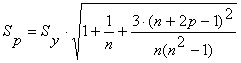
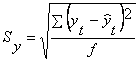
![]()
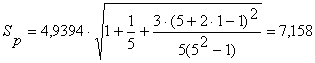
Таблица 3 – Расчеты доверительных интервалов для квадратичного тренда
|
№ п/п (р) |
Точечный
прогноз |
|
|
Доверительные интервалы |
|
|
Минимальный
|
Максимальный
|
||||
|
1 |
130,456 |
7,158 |
19,8992 |
110,564 |
150,3552 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.