Расчет показателей средней ошибки аппроксимации, среднего квадратичного отклонения. Коэффициент парного корреляционного отношения, страница 2

Экстраполяция трендов: Квадратичный тренд

Параметры уравнения определяются с помощью метода наименьших квадратов

Для квадратичного уравнения, система нормальных уравнений имеет такой вид:

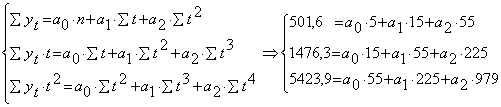
1.Решим уравнение матричным способом:

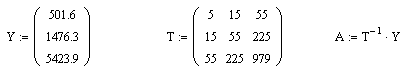
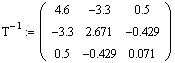
Таким образом уравнение тренда имеет вид:

2. Решим уравнение методом подстановки:
1.Умножим 1-ое уравнение на 3 и вычтем его из 2 – го уравнения

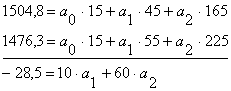
2. Умножим 1-ое уравнение на 11 и вычтем его из 3 – го уравнения

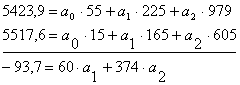
3.Обьеденим 2 полученных уравнения в систему и решим ее:

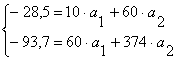
Умножим 1-ое уравнение на 6 и вычтем из 2- го:

Таблица 2- Расчеты для оценки качества уравнения

1 2 3 4