Знак минус в правой часта уравнения определяет наличие и системе главной обратной отрицательной связи.
Уравнение (1) дано в размерных
координатах. Для перехода к безразмерным координатам отнесем входные и
выходные координаты к их номинальным (паспортным) значениям. С этой целью
введем в уравнение (1) новые переменные: 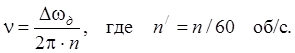
При п = 3000 об/мин, п'
= 50 об/с, откуда 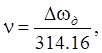 или Dwд = 314.16 v, где
v - безразмерная скорость объекта
регулирования.
или Dwд = 314.16 v, где
v - безразмерная скорость объекта
регулирования.
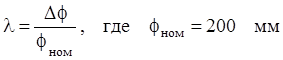 для всех вариантов - номинальный ход регулирующего органа
регулятора, откуда
для всех вариантов - номинальный ход регулирующего органа
регулятора, откуда 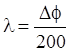 , или
, или ![]() ,
где l -
безразмерный ход регулирующего органа регулятора.
,
где l -
безразмерный ход регулирующего органа регулятора.
Подставив выражения Dwд и Dф, а также численные значения Т0 и К0 в выражение (1), получим дифференциальное уравнение, описывающее динамику объекта регулирования в безразмерных координатах:
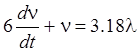
Передаточная функция объекта регулирования
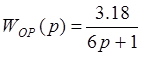
2.2 Динамика датчика скорости регулятора
Математическая модель поведения в переходном процессе центробежного датчика скорости описывается апериодическим звеном второго порядка.
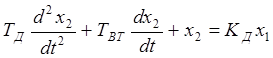
Введем безразмерные координаты и новые переменные:
х2 =
D S - приращение перемещения муфты датчика, х1 = Dwд, 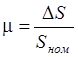 , где
, где ![]() = 20 мм
= 20 мм
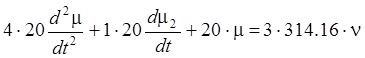 . Тогда
уравнение динамики датчика скорости в размерных координатах
. Тогда
уравнение динамики датчика скорости в размерных координатах
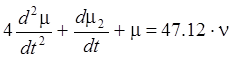
Передаточная функция датчика
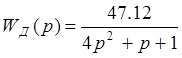
Математическая модель поведения в переходном процессе сервомеханизма регулятора скорости непрямого действия описывается интегрирующим звеном.
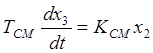
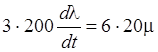 .Тогда уравнение динамики сервомеханизма в
безразмерных координатах:
.Тогда уравнение динамики сервомеханизма в
безразмерных координатах: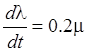
Передаточная функция сервомеханизма:
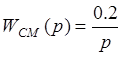
2.4 Динамика местной обратной отрицательной связи
Математическая модель поведения в переходном процессе местной обратной отрицательной связи описывается усилительным или идеальным звеном:
![]() , где
, где 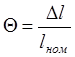 -
безразмерная выходная координата МООС,
-
безразмерная выходная координата МООС, ![]() - её
приращение,
- её
приращение, ![]() = 25 [мм]- её номинальное
значение.
= 25 [мм]- её номинальное
значение.
Передаточная функция МООС
![]()
2.5 Исследование САР с использованием системы MathLAB
2.5.1 Определение передаточной функции разомкнутой САР при известных передаточных функциях элементов структурной схемы
Передаточная функция объекта регулирования
h1=tf(3.18,[6 1])
Transfer function:
3.18
------6 s + 1
Передаточная функция датчика
h2=tf(47.12,[4 1 1])
Transfer function:
47.12
------------4 s^2 + s + 1
Передаточная функция сервомеханизма
h3=tf(0.2,[1 0])
Transfer function:
0.2
--s
Передаточная функция МООС
h4=tf(1)
Transfer function:
1
Передаточная функция регулятора не охваченного МООС
h5=series(h2,h3)
Transfer function:
9.424
--------------4 s^3 + s^2 + s
Передаточная функция регулятора охваченного МООС
h6=feedback(h5,h4)
Transfer function:
9.424
----------------------4 s^3 + s^2 + s + 9.424
Передаточная функция разомкнутой САР
h7=series(h1,h6)
Transfer function:
29.97
----------------------------------------24 s^4 + 10 s^3 + 7 s^2 + 57.54 s + 9.424
2.5.2 Определение коэффициента усиления регулятора
Необходимым и достаточным условием устойчивости системы является наличие либо отрицательных вещественных, либо комплексных с отрицательной вещественной частью корней характеристического уравнения дифференциального уравнения свободного движения системы. Будем определять оптимальный коэффициент усиления регулятора методом корневого годографа, сущность которого состоит в выборе оптимальных значений корней обеспечивающих заданную устойчивость системы. В качестве задания устойчивости в данном случае используется коэффициент демпфирования. Примем его x= 0.7
rlocus(h7), sgrid
k=rlocfind(h7)
Select a point in the graphics window
selected_point = -1.2373 + 0.9284i
k = 5.3383
2.5.3 Определение динамических параметров САР
Передаточная функция разомкнутой САР с найденным коэффициентом усиления регулятора
H=series(h7,k)
Transfer function:
160
----------------------------------------24 s^4 + 10 s^3 + 7 s^2 + 57.54 s + 9.424
Построение годографа Найквиста
nyquist(H), grid
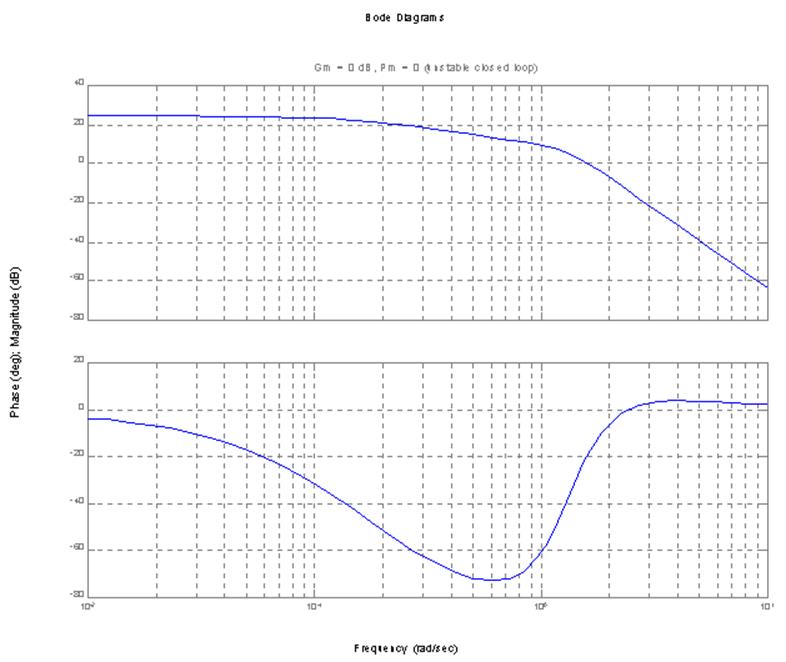
Построение диаграмм Боде
bode(H)
Определение запасов устойчивости по фазе и модулю
margin(H)
Передаточная функция замкнутой САР
H1=feedback(H,k)
Построение переходной функции
step(H1)
Приложение А
Определение коэффициента усиления регулятора
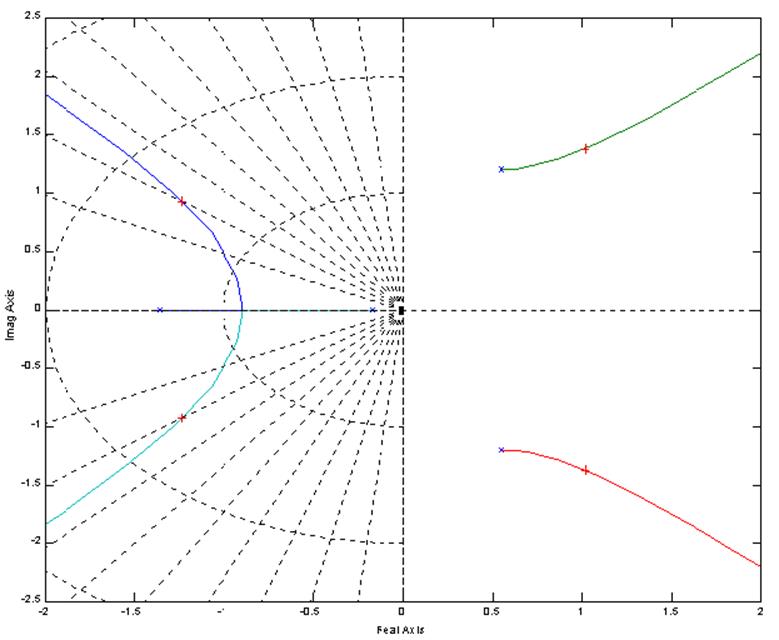
Приложение Б
Годограф Найквиста
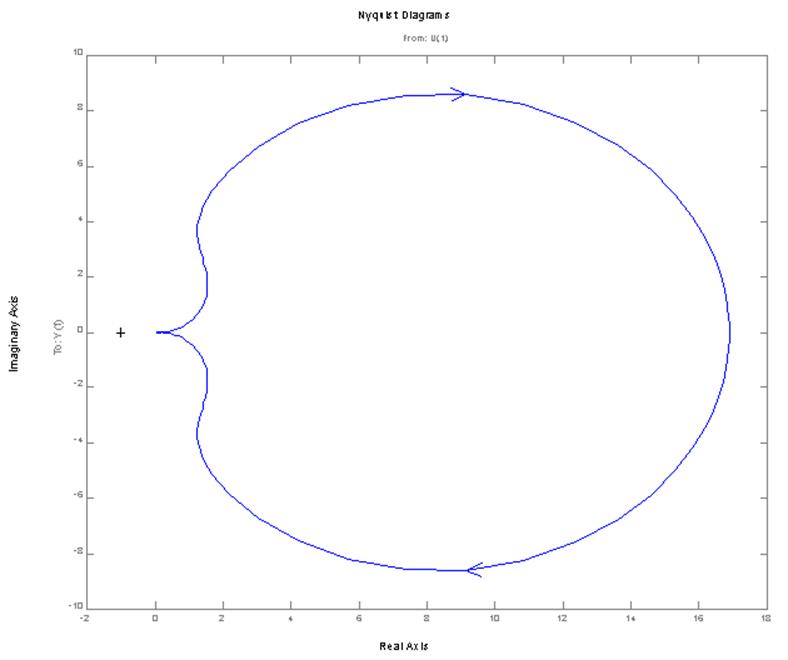
Приложение В
Диаграммы Боде
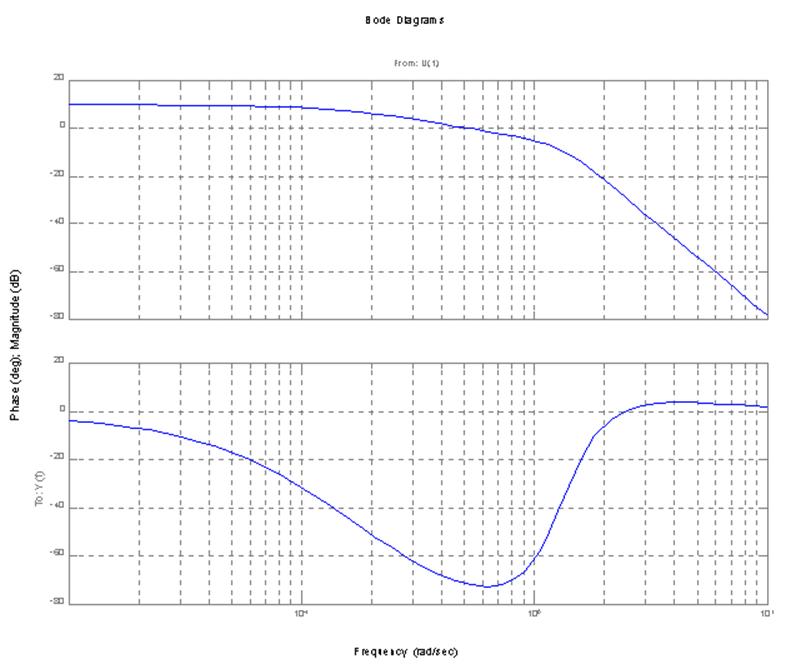
Приложение Г
График переходного процесса
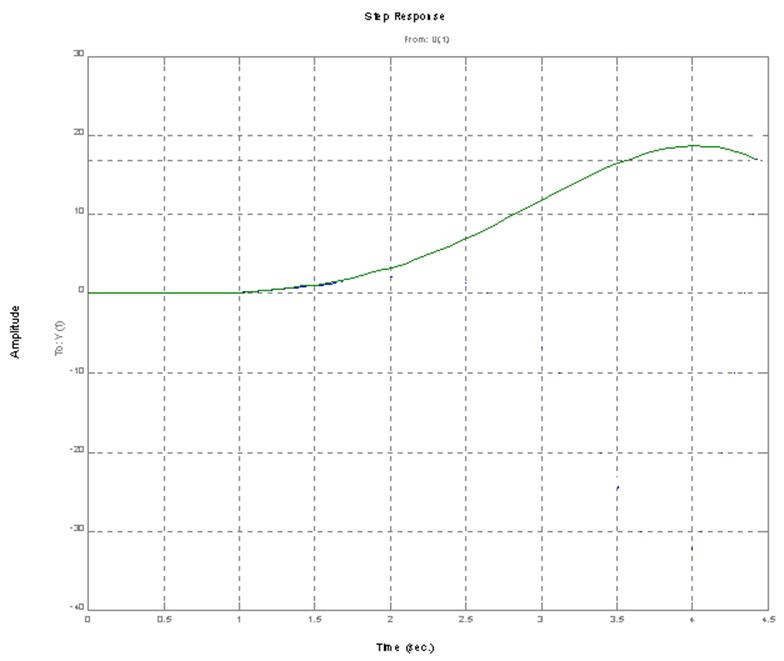
Список использованных источников
1. Левин М.И. Автоматизация судовых энергетических установок: Л.: Судостроение 1969.- 469 с.
Приложение В
Диаграммы Боде
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.