Моделирование типовых динамических функций в системе MatLAB

 

Министерство образования Российской Федерации

Государственное образовательное учреждение

высшего профессионального образования

“Комсомольский-на-Амуре государственный

технический университет”

Кафедра “Судовые энергетические установки”

Лабораторная работа №1

Моделирование типовых динамических

функций в системе MatLAB

Студент группы 0ТЭ                                                    А.В. Балута

Преподаватель                                                              А.А. Малыхин

2004

 

Содержание

Содержание……………………………………………………………………………2

1.  Понятие типовой динамической функции (т.д.ф.)………………………………3

2.  Цель введения т.д.ф………………………………………………………………..3

3.  Таблица……………………………………………………………………………..3

4.  Программы…………………………………………………………………………4

5.  Графики переходных процессов т.д.ф……………………………………………4

 

1.  Понятие типовой динамической функции

Типовая динамическая функция есть математическая модель реального технического устройства или его части, описывающая его поведение в нестационарном динамическом режиме дифференциальными уравнениями не выше 2-ого порядка и имеющая типовую форму переходного процесса.

Передаточной функцией звена или системы называется отношение преобразованной по Лапласу величины на выходе к преобразованной по Лапласу величине на входе звена или системы при нулевых начальных условиях.

2.  Цель введения типовой динамической функции

Любая динамическая система, т.е. система, работающая при изменяющихся внешних воздействиях, в том числе и САР, состоят из отдельных звеньев. Эти звенья, как входящие в конкретную систему, так и в многочисленные другие системы, отличаются друг от друга по используемым физическим принципам работы, по конструкции, а иногда и по другим параметрам.

Исследовать динамику отдельного звена означает определить по какому закону будет изменяться выходной параметр “y” во времени при известном изменении входного параметра, т.е. сводится к нахождению зависимости:

y = f(x,t)

На первом этапе использования и исследования САР при нахождении таких уравнений исходили из физического принципа работы и конструкции звена. Подобный подход был не только трудоемкий, но и требовал заново решать все возникающие задачи при изменении используемого принципа или конструкции звена.

Решение задач динамики существенно упростились, когда в ходе многочисленных экспериментов обратили внимание на то, что если на вход различных звеньев подать одинаковые по форме входные сигналы и каким-либо способом записать выходные сигналы во времени, то число форм выходных кривых оказалось удивительно невелико. Следовательно, возникает возможность заменить многочисленные реальные звенья небольшим числом их математических моделей. Так возникло понятие типовой динамической функции.

3.  Таблица

№	Наименование звена	Передаточная функция	П.ф. в системе MatLAB
1	Апериодическое звено 1-ого порядка	W(p) = k/(Tp+1)	h1=tf(5,[2 1])
2	Апериодическое звено 2-ого порядка	W(p) = k/(T1p+T2p+1)	h2=tf(5,[0.25 2 1])
3	Колебательное звено	W(p) = k/(T1p+T2p+1)	h3=tf(5,[4 2 1])
4	Интегрирующее звено	W(p) = k/Tp	h4=tf(5,[2 0])
5	Дифференцирующее звено	W(p) = kp/(Tp+1)	h5=tf([5 0],[2 1])

 

4.  Программа

h1=tf(5,[2 1])                 % передаточная функция апериодического звена 1-ого порядка

step(h1)

h2=tf(5,[0.25 2 1])         % передаточная функция апериодического звена 2-ого порядка

step(h2)

h3=tf(5,[4 2 1])              % передаточная функция колебательного звена

step(h3)

h4=tf(5,[2 0])                 % передаточная функция интегрирующего звена

step(h4)

h5=tf([5 0],[2 1])           % передаточная функция дифференцирующего звена

step(h5)

5.  Графики переходных процессов т.д.ф

1.  График переходного процесса апериодического звена 1-ого порядка

 

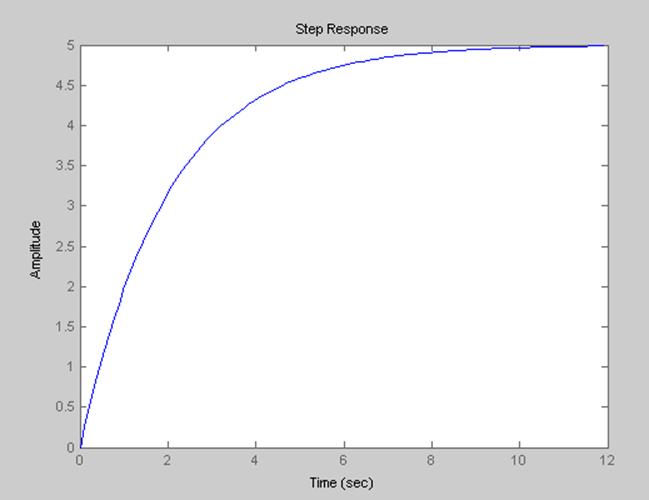
2.   График переходного процесса апериодического звена 2-ого порядка

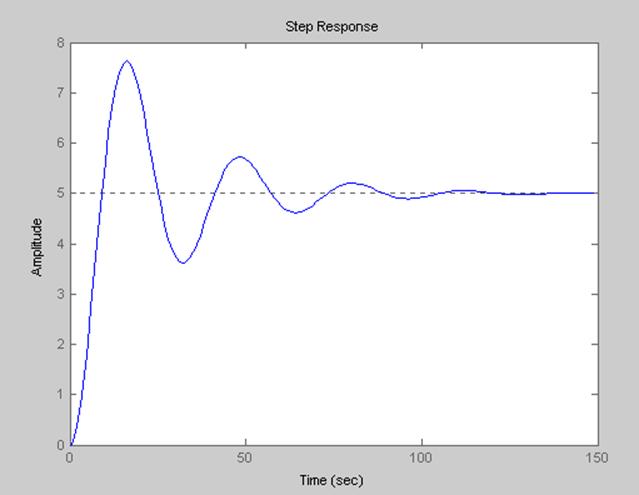
3.  График переходного процесса колебательного звена

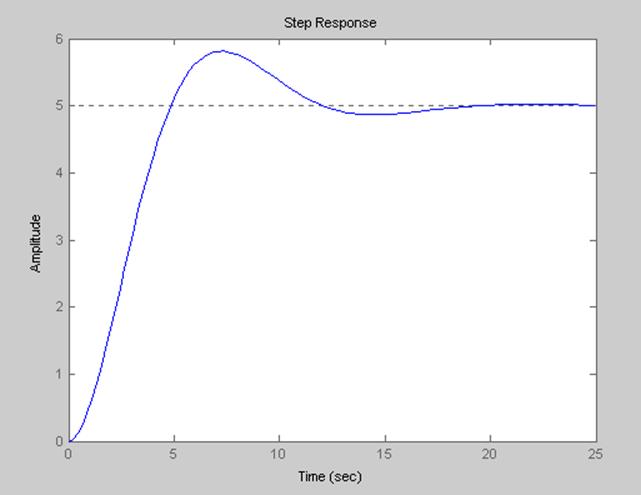
4.  График переходного процесса интегрирующего звена

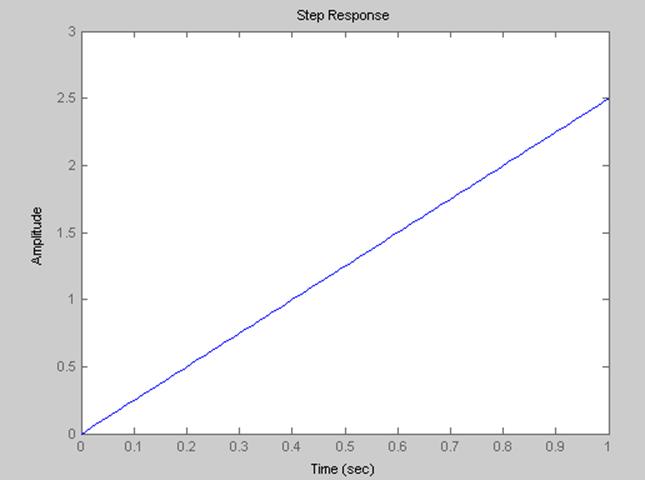
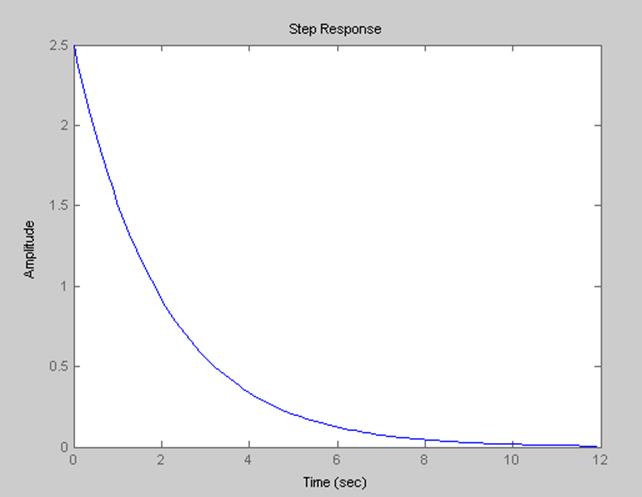
5.  График переходного процесса дифференцирующего звена