Распределение полезной разности температур может быть выполнено:
1) при условии равенства поверхности нагрева корпусов;
2) при условии минимальной суммарной поверхности нагрева корпусов;
3) при минимальной общей поверхности нагрева аппаратов и одинаковой их поверхности;
4) исходя из заданных давлений (температур) вторичного пара в корпусах выпарной установки.
В соответствии с уравнением (24.20) полезная разность температур по корпусам определяется следующими выражениями:
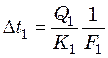 ; (25.6)
; (25.6)
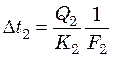 ; (25.7)
; (25.7)
. . . . . . . . . . . .
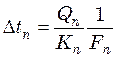 . (25.8)
. (25.8)
По условию, ![]() , следовательно, складывая левые
и правые части уравнений (25.6) – (25.8) и заменяя
, следовательно, складывая левые
и правые части уравнений (25.6) – (25.8) и заменяя ![]() ,
получим:
,
получим:
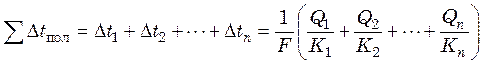 , (25.9)
, (25.9)
откуда 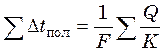 (25.10)
(25.10)
и 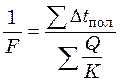 . (25.11)
. (25.11)
Подставим полученное значение для ![]() в
уравнения (25.6) – (25.8)
в
уравнения (25.6) – (25.8)
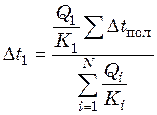 ;
; 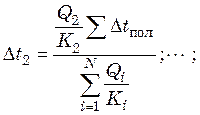
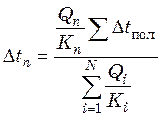 . (25.12)
. (25.12)
С другой стороны, при равной поверхности нагрева корпусов
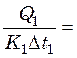
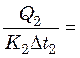
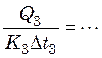
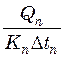 (25.13)
(25.13)
или
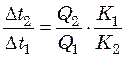 ;
; 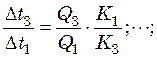
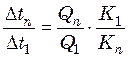 . (25.14)
. (25.14)
Соотношения (25.14) показывают, что для достижения равных поверхностей нагрева всех корпусов установки необходимо, чтобы отношения их полезных разностей температур были прямо пропорциональны тепловым нагрузкам корпусов и обратно пропорциональны их коэффициентам теплопередачи.
Рассмотренный вариант распределения полезной разности температур является наиболее распространенным на практике, так как при этом обеспечивается удобство монтажа и обслуживания одинаковых аппаратов, а также их взаимозаменяемость.
Для вывода уравнения распределения полезной разности температур многокорпусной выпарной установки, при условии минимальной суммарной поверхности нагрева корпусов, выразим суммарную поверхность установки следующим уравнением:
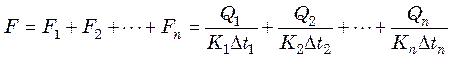 . (25.15)
. (25.15)
В уравнении (25.15) величины ![]() и
и ![]() , так же как и поверхность
, так же как и поверхность ![]() , являются функциями разности температур, а
установить эту зависимость на данном этапе расчета, очень сложно. Поэтому будем
оперировать средними их значениями, так как при этом тепловую нагрузку и
коэффициент теплопередачи можно считать постоянными величинами и суммарная
поверхность нагрева аппарата остается функцией
только полезной разности температур по корпусам установки.
, являются функциями разности температур, а
установить эту зависимость на данном этапе расчета, очень сложно. Поэтому будем
оперировать средними их значениями, так как при этом тепловую нагрузку и
коэффициент теплопередачи можно считать постоянными величинами и суммарная
поверхность нагрева аппарата остается функцией
только полезной разности температур по корпусам установки.
Для упрощения вывода рассмотрим двухкорпусную выпарную установку. Из
уравнения (25.15) с учетом того, что ![]() , получим:
, получим:
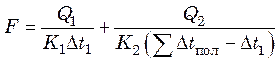 . (25.16)
. (25.16)
Минимальную поверхность нагрева определяем в результате исследования
функции ![]() на экстремум:
на экстремум:
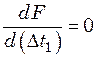 ; (25.17)
; (25.17)
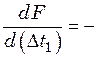
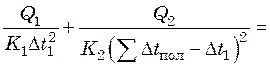
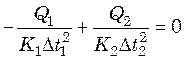 (25.18)
(25.18)
или 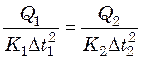 , (25.19)
, (25.19)
откуда 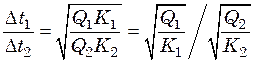 . (25.20)
. (25.20)
Из уравнения (25.20) следует, что для достижения минимальной общей поверхности нагрева многокорпусной выпарной установки отношение полезных разностей температур в любых двух аппаратах должно быть прямо пропорционально корню квадратному из отношения тепловых нагрузок этих корпусов и обратно пропорционально корню квадратному из отношения их коэффициентов теплопередачи.
По свойству пропорции
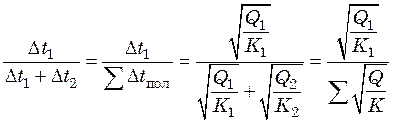 . (25.21)
. (25.21)
Следовательно, для первого корпуса
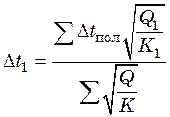 . (25.22)
. (25.22)
Аналогично для второго корпуса
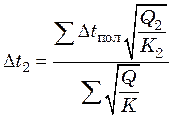 . (25.23)
. (25.23)
Для ![]() -го корпуса выпарной установки
-го корпуса выпарной установки
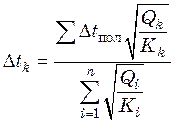 . (25.24)
. (25.24)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.