Основы расчета массообменных аппаратов, страница 3

Таким образом, h_л учитывает понижение эффективности массопередачи в рассматриваемой точке ступени за счет того, что не достигается равновесие между контактирующими фазами.

Коэффициент полезного действия ступени η_т учитывает влияние того же фактора, но по отношению ко всей ступени в целом:

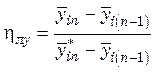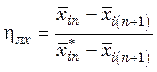                     ;   ,                  (31.14)

где  и  – средние составы фаз, выходящих из n-й ступени;  и  – средние составы фаз, поступающих в n-ю ступень;  – состав фазы Ф_у, находящейся в равновесии с фазой Ф_х состава;  – состав фазы Ф_х, равновесной с фазой Ф_у состава.

Величины h_л и h_т разнятся тем значительней, чем больше изменяются составы материальных потоков по длине или сечению ступени (тарелки). Связь между ними определяется структурой потоков. При полном смешении фазы Ф_у в случае линейной равновесной зависимости анализ условий взаимодействия фаз приводит к следующей зависимости:

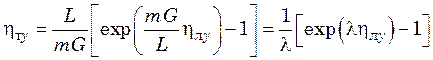             ,          (31.15)

где 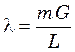; m и  – углы наклона равновесной и рабочей линии соответственно.

Так как L/G может быть больше единицы, то, как следует из уравнения (31.15), при h_лу > 1 величина h_ту может быть также больше единицы.

При идеальном перемешивании обеих фаз η_л = η_т.

Под коэффициентом полезного действия аппарата h_к подразумевают обычно отношение числа теоретических ступеней контакта фаз N_т к числу реальных ступеней N_д, обеспечивающих одинаковые составы материальных потоков на выходе аппарата при одинаковых расходах и составах материальных потоков на его входе,

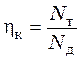                                          .                                       (31.16)

Коэффициенты полезного действия h_л, h_т и h_к, так же как коэффициент массопередачи и число единиц переноса, являются кинетическими характеристиками. Величина их зависит от взаимного направления движения фаз и степени перемешивания каждой фазы на ступени (тарелке). Зависимость между указанными кинетическими характеристиками определяется следующими соотношениями.

При полном перемешивании обеих фаз их концентрации постоянны и равны конечным (х = х_к; у = у_к; Δу = у_к* – у_к). На любой тарелке при принимающей фазе Ф_у

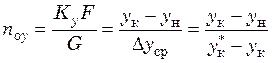                          .                       (31.17)

Если к знаменателю последней дроби прибавить и вычесть у_к, а затем разделить числитель и знаменатель новой полученной на (у_к – у_н), то

   

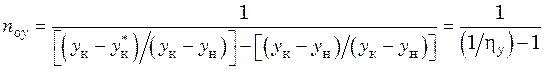
либо

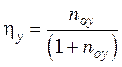                                       .                                    (31.18)

Аналогично для фазы Ф_х

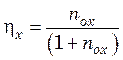                                       .                                   (31.19)

При полном перемешивании жидкой фазы и движении газовой (паровой) фазы в режиме идеального вытеснения, принимая х = х_к = const и у* = у_к* при m = const

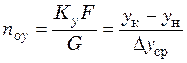                                  ,                              (31.20)

где 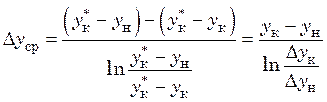                .                  (31.21)

Из сопоставления уравнений (31.20) и (31.21) получаем

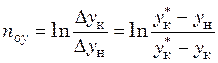                               .                            (31.22)

Воспользовавшись тем же приемом, что и в предыдущем случае, т.е. прибавив и вычтя из знаменателя последней дроби у_н, а затем разделив числитель и знаменатель вновь полученной дроби на числитель, получим:

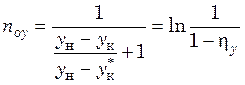                                                       (31.23)

либо h_у = 1 – exp(–n_oy).

Связь между коэффициентом массопередачи K_у, высотой эквивалентной теоретической тарелки h_экв и высотой единицы переноса h_оу при m= const может быть определена, исходя из следующего.

Количество вещества, перешедшего из фазы Ф_у в фазу Ф_х на любой i-й теоретической тарелке,

                        ,                     (31.24)

где F – площадь поперечного сечения колонны; Δу_iср – средняя движущая сила на i-й тарелке:

                            

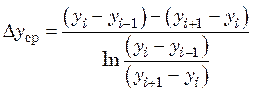
(индекс i–1 соответствует вышележащей тарелке по ходу фазы Ф_у, а индекс i+1 – нижележащей).

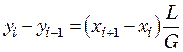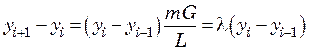В соответствии с материальным балансом i-й тарелки , в то же время при m = const . Следовательно,  и .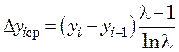

Подстановка последнего выражения в уравнение (31.24) дает

                           ,

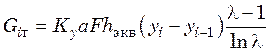отсюда

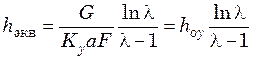                            .                         (31.25)

Если равновесная зависимость нелинейна (m ≠ const), то связь между указанными характеристиками более сложная.

31.4 Определение числа реальных ступеней контакта
фаз

Используя число единиц переноса либо КПД ступени (тарелки), можно графически, а в случае m = const и аналитически, определить число действительных ступеней или тарелок N_д.