ЛЕКЦИЯ 29
Подобие процессов переноса массы. Коэффициент ы массопередачи
Наиболее строгий и принципиально возможный путь для определения коэффициентов массоотдачи заключается в интегрировании уравнения диффузии в движущейся среде совместно с уравнениями движения, т. е. с уравнениями Навье – Стокса и уравнением неразрывности потока при заданных начальных и граничных условиях.
Однако система указанных уравнений практически не имеет общего решения. Поэтому так же, как для гидродинамических и теплообменных процессов, не решая системы основных уравнений, можно методами теории подобия найти связь между переменными, характеризующими процесс переноса в потоке фазы, в виде обобщенного (критериального) уравнения массоотдачи.
В это уравнение входят критерии подобия, которыми описывается подобие процессов массоотдачи на границе фазы (подобие граничных условий) и в основной массе (ядре) фазы.
29.1. Вывод основных критериев подобия
При наличии пограничного слоя, в котором перенос осуществляется молекулярной
диффузией, количество вещества, переходящего из ядра к границе фазы составит ![]() .
.
То же количество вещества переносится молекулярной диффузией через
пограничный слой и согласно первому закону Фика 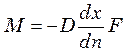 .
.
Приравнивая правые части последних равенств, получим подобие условий переноса на границе фазы:
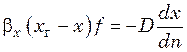 либо
либо
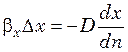 . (29.1)
. (29.1)
Заменив в уравнении (29.1) dx на Δx, а dn на характерный линейный размер l, а также поделив левую часть уравнения на правую и опустив знак «минус», имеем для подобных систем
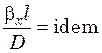 . (29.2)
. (29.2)
Полученный комплекс величин носит название диффузионного критерия Нуссельта
(Nuд) (в англоязычной литературе критерий Шервуда ![]() ):
):
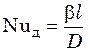 . (29.3)
. (29.3)
Критерий Нуссельта Nuд является отношением интенсивности переноса вещества в ядре фазы (b) к интенсивности его переноса в пограничном диффузионном подслое (D) и выражает подобие переноса вещества у границы фазы в сходственных точках подобных систем.
Подобие процессов переноса вещества в ядре фазы устанавливается с помощью дифференциального уравнения нестационарной диффузии в движущейся среде. Для одномерного переноса вещества вдоль оси х уравнение нестационарной диффузии может быть записано следующим образом:
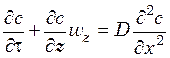 , (29.4)
, (29.4)
где ![]() –
изменение концентрации вещества во времени;
–
изменение концентрации вещества во времени; 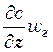 –распределение
концентрации вещества в потоке за счет конвективной диффузии;
–распределение
концентрации вещества в потоке за счет конвективной диффузии; 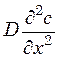 – распределение концентрации вещества
за счет молекулярной диффузии.
– распределение концентрации вещества
за счет молекулярной диффузии.
Опустив знаки операторов, уравнение (29.4) можно представить в виде выражения
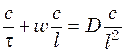 ,
,
где l ‑ характерный линейный размер.
Далее, в соответствии с общими принципами вывода критериев подобия,
поделив левую часть последнего равенства на его правую часть, получим комплексы![]() и
и ![]() .
Комплекс
.
Комплекс ![]() носит название диффузионного критерия Фурье
(Foд). Обычно его представляют в виде обратной величины, т.е.
носит название диффузионного критерия Фурье
(Foд). Обычно его представляют в виде обратной величины, т.е.
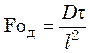 . (29.5)
. (29.5)
Равенство критериев Foд в сходных точках подобных систем является необходимым условием подобия неустановившихся процессов массопередачи. Это равенство характеризует постоянство отношения изменения концентрации вещества во времени к изменению его концентрации вследствие
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.