Аналіз потоку вимог на технічне обслуговування і ремонт автомобілів

3.  Науково-дослідна частина

Аналіз потоку вимог на технічне обслуговування і ремонт автомобілів

Першим і необхідним завданням при практичному використанні теорії масового обслуговування є вивчення потоку вимог, його треба вміти описати кількісно.

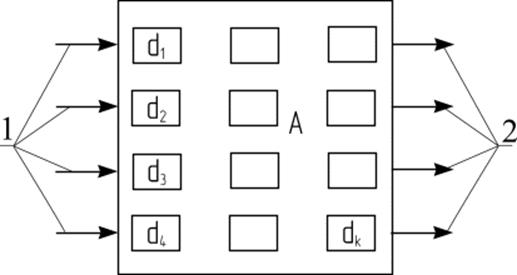
Рис.1 Схематичне зображення систем масового

обслуговування:

– обслуговуючі апарати;

А– обслуговуюча система;

1, 2– вхідні та вихідні потоки

Процес ТО і ремонту автомобільної техніки має елементи випадковості. Відкази і несправності автомобілів, скасування і затримки рейсів автобусів, недоліки у постачанні обмінним фондом агрегатів і запасними частинами та інші причини породжують нерегулярність надходження автомобілів на обслуговування і несталість обсягу виконуваних робіт.

Надалі під вимогою розумітимемо автомобіль, який потребує ТО, під обслуговуючим апаратом — бригаду виконавців робіт на ТО автомобілів, засоби, потрібні для механізації робіт на ТО автомобілів, а під системою масового обслуговування — ремонтно-обслуговуюче виробництво АТП.

З метою спрощення розв'язування практичних завдань у багатьох випадках беруть найпростіший потік вимог, що задовольняє умови стаціонарності, ординарності та відсутності післядії.

Стаціонарність потоку означає, що інтенсивність потоку вимог протягом розглядуваного періоду стала. Ординарність потоку виражає собою практичну неможливість появи двох і більше вимог за досить малий проміжок часу, тобто одночасно може надійти не більше однієї вимоги на обслуговування. Відсутність післядії (взаємозалежності) означає, що кількість вимог, які надійшли до системи після довільного моменту , не залежить від того, скільки вимог надійшло до системи до моменту , тобто взаємонезалежно. Потоки, що відповідають цим умовам, називають пуассонівськими.

Імовірність надходження  вимог найпростішого потоку за час  визначають за формулою Пуассона:

де: — середня кількість вимог на обслуговування, які надходять за одиницю часу (інтенсивність потоку).

З часом інтенсивність потоку може не залишатися сталою. Наприклад, інтенсивність потоку вимог на обслуговування автомобілів удень менша, ніж увечері. Природно, що й організація обслуговування, яка є оптимальною при денній інтенсивності потоку вимог, не буде оптимальною при вечірній. Тому для правильної організації обслуговування треба виділяти періоди з приблизно однаковою інтенсивністю потоку і вирішувати виникаючі завдання для кожного з них.

В умовах АТП часто трапляються потоки вимог з обмеженою післядією. Це означає, що момент появи чергової вимоги залежить тільки від того, коли надійшла попередня, і не залежить від того, як чергувались вимоги раніше, тобто вплив усього потоку на момент появи чергової вимоги обмежений тільки останньою вимогою. Такі потоки позначають символом GІ.

Проміжки часу між послідовними надходженнями вимог величини випадкові. Для повного їх опису треба вказати не тільки середню довжину проміжків, а й розподіл проміжків, тобто зазначити, як часто вони набирають тих чи інших числових значень.

Пояснимо це на прикладі. На одному з АТП у вечірній   час надійшло на ТО-1  40 автомобілів. Проміжки  між  надходженнями  автомобілів,  хв., були такі:  2,   17,  1, 10, 2, 3, 1, 1, 13, 4, 2,  1, 3, 8,  1, 2, 5,  10, 5, 14,  10, 5,  1, 6, 7, 1, 31, 5, 27, 17, 4, 5, 5, 1, 2, 1, 8, 1, 7, 8.

Виберемо трихвилинні інтервали часу й позначимо через  і , початок і кінець -го інтервалу ( = 1, 2, ...). Визначимо кількість вимог, які потрапили в кожен інтервал, тобто частоту  надходження вимог в -му інтервалі.

Якщо частоту  поділимо на довжину інтервалу (—) і на загальну кількість заїздів, що дорівнює 40, то дістанемо відносну випадковість у заданому інтервалі.

Результати розрахунків зведемо в таблицю 1

Таблиця 1

Використовуючи ці значення, відкладемо на осі абсцис (рис. 3.2) границі інтервалів, а на осі ординат — відносні частоти. Побудуємо в цих координатах гістограму  за формулою:

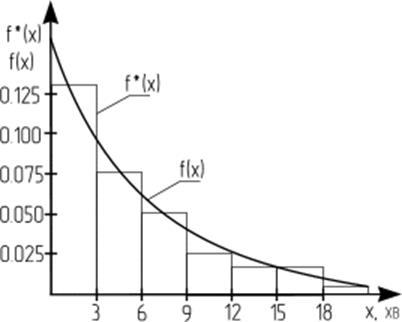
Рис.2 Гістограма  і щільність розподілу проміжків часу між надходженнями вимог на ТО-1 автомобілів

Добута гістограма дає наочне уявлення про розподіл проміжків часу між надходженнями вимог на ТО-1. Ступінчасту криву  згладимо неперервною кривою . При достатньо малому значенні  площа  дорівнює ймовірності того, що час між надходженнями вимог лежить в інтервалі від  до ( + ).

Функцію  називають щільністю розподілу розглядуваної випадкової величини. Вона визначає закон розподілу, оскільки показує, з якою ймовірністю ця величина набирає тих чи інших значень. У нашому прикладі гістограма  добре згладжується експоненціальною кривою. Це дає змогу дійти висновку, що проміжки часу між надходженнями автомобілів (вимог) та ТО-1 мають експоненціальний розподіл:

де: — параметр розподілу, що дорівнює середній кількості вимог, які надходять на обслуговування за одиницю часу.

У наведеному прикладі середній час між надходженнями автомобілів на ТО-1 дорівнює 6 хв. Тоді інтенсивність потоку вимог за одиницю часу (одну хвилину):

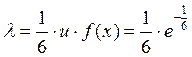
Розглянутий нами потік без післядії пуассонівський. Його позначають символом М.

В окремому випадку може бути потік, у якому вимоги з'являються через сталі проміжки часу. Такий потік називають детермінованим і позначають символом D.

У разі детермінованого потоку знання моменту появи чергової вимоги дає змогу цілком точно визначити момент появи наступного, чого не можна зробити при потоці М. При ординарному стаціонарному потоці без післядії (пуассонівському) навіть знання того, скільки часу минуло з моменту появи останньої вимоги, не дає додаткової інформації про момент появи чергової.

У потоках з обмеженою післядією інтервали часу між надходженнями вимог несталі і не розподілені експоненціально. Вид розподілу визначають за гістограмою, яку будують за результатами обробки статистичної інформації.

Для оцінки показника випадковості або, навпаки, регулярності потоку можна використати середнє квадратичне відхилення проміжків часу між надходженнями вимог :

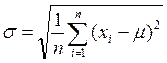
де: — загальна  кількість проміжків;

— зареєстровані значення проміжків;

— середнє значення проміжків;

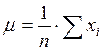
Середнє квадратичне відхилення  є мірою розкиду розглядуваної випадкової величини біля її середнього значення. Для суто випадкових потоків (проміжки часу між надходженнями вимог розподілені експоненціально)  = (розкид великий), для детермінованих— =0 (розкиду немає), для потоків проміжного типу — >>0.