














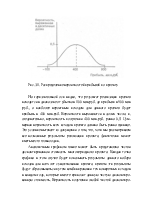







Исходя из изложенного, мы можем получить средний результат проекта, взвешивая каждый возможный исход от его вероятности и складывая эти суммы для каждого исхода.
Средний чистый доход от проекта на нашем графике составляет 400 млн.руб. Эта величина представляет собой среднее или центральное значение распределения вероятностей проекта и обычно называется математическим ожиданием (expected value) проекта.
Риск, связанный с проектом, обычно рассматривается в литературе по оценке и отбору проектов как возможное рассеяние результатов относительно этого значения. Данная мера риска обладает определенной привлекательностью для многих людей, поскольку измерение разброса или дисперсии распределения математического ожидания указывает на вероятное отклонение фактического результата от его "наиболее оптимистического" прогноза.
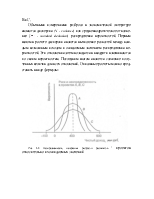
Смысл такого подхода к риску можно проиллюстрировать графиком (рис.3.2), на котором представлены распределения вероятностей результатов различных проектов.
Все три проекта имеют одинаковое математическое ожидание, равное 400 млн.руб. Проект С был показан на предыдущем графике. Анализируя график 3.2., многие будут рассматривать проект В как менее рискованный, чем проект С, поскольку крайние значения первого проекта расположены ближе к среднему значению и больше вероятность получения математического ожидания в 400 млн.руб. Исходя из таких же критериев, можно сказать, что проект А лучше проектов В и С.
Обычными измерениями разброса в экономической литературе являются дисперсия (V - variance) или среднеквадратическое отклонение (![]() -
standard deviation) распределения вероятностей. Первым шагом в расчете дисперсии является вычисление
разностей между каждым возможным исходом
и ожидаемым значением распределения вероятностей. Эти отклонения затем
возводятся в квадрат и взвешиваются
по своим вероятностям. Последним шагом является сложение полученных величин для всех отклонений. Описанные
расчеты можно представить в виде
формулы:
-
standard deviation) распределения вероятностей. Первым шагом в расчете дисперсии является вычисление
разностей между каждым возможным исходом
и ожидаемым значением распределения вероятностей. Эти отклонения затем
возводятся в квадрат и взвешиваются
по своим вероятностям. Последним шагом является сложение полученных величин для всех отклонений. Описанные
расчеты можно представить в виде
формулы:
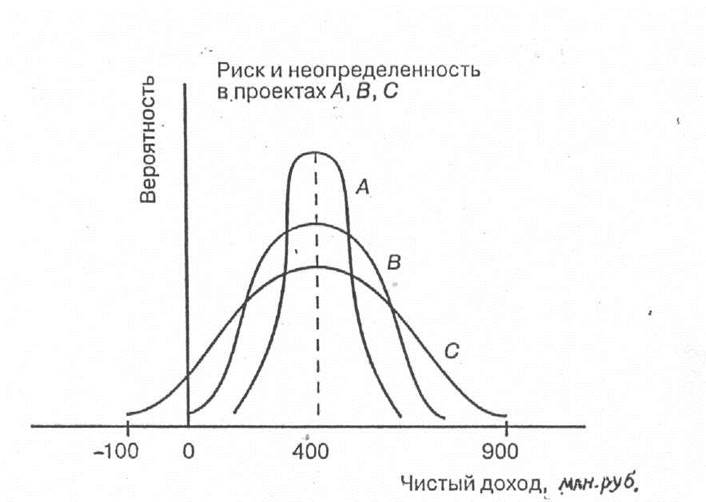
Рис. 3.2. Неопределенность, измеряемая разбросом результатов ' проектов относительно их ожидаемых значений
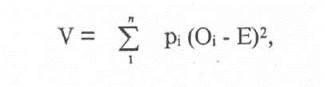
где Oi - возможный результат;
Е - математическое ожидание распределения вероятностей
(expected value of probability distribution); pi - вероятность (likelihood) результата Oi.
Знак ![]() означает, что все
возведенные в квадрат и взвешенные по своим вероятностям квадратичные отклонения должны быть сложены.
Среднеквадратическое отклонение
означает, что все
возведенные в квадрат и взвешенные по своим вероятностям квадратичные отклонения должны быть сложены.
Среднеквадратическое отклонение ![]() распределения вероятностей
определяется, как квадратный корень из дисперсии:
распределения вероятностей
определяется, как квадратный корень из дисперсии:
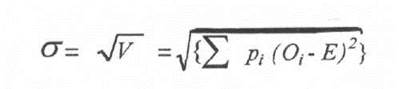
Следовательно, связанная с проектом неопределенность, обычно определяемая дисперсией или среднеквадратическим отклонением, зависит от нашей интерпретации вероятностей.
До самого последнего времени в статистике концепция вероятности основывалась на классической частотной интерпретации (frequency interpretation), с которой происходит данное событие. Основанные на частотах веротности называют объективными
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.