Моделювання й оптимізація апаратів: Методичні вказівки до виконання контрольної (практичної) роботи з дисципліни “Теорія технічних систем”, страница 4

Форма завдання наведена в додатку А.

3  Послідовність виконання контрольної роботи

Під час виконання контрольної роботи необхідно розв’язати дві задачі оптимізації, які наводяться в порядку збільшення складності математичних моделей у наступній послідовності:

1.  Оптимізація розмірів відкритого збірника.

2.  Оптимізація витрат на створення й експлуатацію трубопроводу.

Методику розв’язання даних задач наведено нижче.

3.1 Оптимізація розмірів відкритого збірника

У бланку завдання наведені всі необхідні дані для розв’язання задачі оптимізації розмірів відкритого збірника.

Математична модель збірника, яка виражає залежність його об'єму від довжини L, ширини B і висоти H, має вигляд

V = L×B×H.                                                     (7)

Збірник матиме мінімальну масу в тому випадку, якщо його сумарна площа поверхні дна і стінок буде мінімальною. Задача полягає в мінімізації цільової функції, яка виражає цю поверхню:

F(L, B, H) = L×B+2×L×H+2×B×H.                             (8)

Вид обмеження f(L, B, H) = 0, тобто f(L, B, H) = L×B×H - V.

Ця задача може бути розв’язана аналітичним методом, наприклад, методом множників Лагранжа. Для цього вводимо допоміжну функцію виду

j(L, B, H, l) = F(L, B, H) + l(L, B, H -V)                        (9)

або

j(L, B, H, l) = L×B+2×L×H+2×B×H+l( L×B×H -V).                          (10)

Знаходимо часткові похідні цієї функції за L, B, H, l і прирівнюємо їх до нуля:

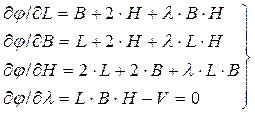(11)

Для визначення значень L, B, H розв’язуємо систему одержаних рівнянь алгебри. Із першого рівняння системи знаходимо

l=(B+2×H)/(B×H).                                         (12)

Визначивши l з другого рівняння системи і прирівнявши до одержаного раніше, знаходимо L=В.

Із третього рівняння системи знаходимо l = –4/В (з урахуванням того, що L=В). Тоді з першого рівняння виходить, що B=2×H.

Отже,

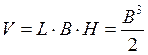, звідки                                 (13)

;                                            (14)

L=B;                                                        (15)

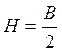.                                                (16)

Тоді сумарна площа поверхні дна і стінок збірника

.                                 (17)

Після знаходження загальної площі дна і стінок оптимізованого збірника необхідно порівняти її з площею збірника без проведення оптимізації з припущенням, що L=B=H, в цьому випадку

                                      (18)

тоді

F = 5×L².                                     (19)

Згідно отриманих результатів необхідно зробити відповідні висновки.

3.2 Оптимізація витрат на створення й експлуатацію трубопроводу

 

Вихідні дані для розв’язання задачі оптимізації витрат на створення та експлуатацію трубопроводу наведені в завданні, а продуктивність насоса залежно від параметрів трубопроводу – в додатку Б.

Для трубопроводу основним параметром є його діаметр, оскільки він визначає масу і вартість трубопроводу (капітальні витрати), а також втрату в ньому тиску на подолання гідравлічного опору. Витрата і вартість електроенергії є складовими експлуатаційних витрат. Чим менший діаметр трубопроводу, тим він дешевший, але при цьому через необхідність збільшення швидкості рідини в ньому збільшуються гідравлічний опір і витрати електроенергії, яка споживається насосом для його подолання.

Для визначення оптимального діаметра трубопроводу доцільно застосувати критерій приведених розрахункових витрат, оскільки він ураховує капітальні й експлуатаційні витрати.

Цільова функція цього критерію стосовно трубопроводу має вигляд

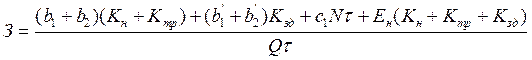,       (20)

де З – приведені розрахункові витрати, грн/м³;

t – час роботи, год. (згідно із завданням);

 – норма амортизаційних відрахувань устаткування і будівель ;

 – норма експлуатаційних витрат устаткування та будівель ;

К_н, К_тр, К_зд – капітальні витрати на насос, трубопровід і будівлю, грн.;

с₁ – вартість 1 кВт×год електроенергії, грн/кВт×год (с₁=0,25 грн.);

N – електрична потужність, споживана насосом, кВт;

Ен – нормативний коефіцієнт ефективності капіталовкладень (Ен=0,17);

Q – витрата продукту, м³/год.

Параметри К_н, К_тр, К_зд, N, Q, що входять у цільову функцію, визначаються з математичної моделі насоса і трубопроводу, що складається з наступних виразів. Капітальні витрати на трубопровід діаметром d_тр=0,15…0,25 м обчислюються за формулою, одержаною апроксимацією даних прейскурантів цін,

,    (21)

де А – коефіцієнт, що враховує подорожчання трубопроводу за наявності термоізоляції (А = 1,1-1,2);