Основы проектирования и конструирования: Методические указания к выполнению лабораторных работ

других элементов конструкций и передающими их тем частям, которые поддерживают балку (чаще всего опорам).

На расчетной схеме балку заменяют ее осью. При этом все нагрузки должны быть приведены к оси балки; силовая плоскость будет совпадать с плоскостью чертежа.

Внешние нагрузки, деформирующие конструкцию (балку) и учитываемые в ее расчете, являются неотъемлемой частью расчетной схемы. Внешние нагрузки в расчетных схемах представляются упрощенно. Различают три вида нагрузок:

·  сосредоточенные силы;

·  распределенная нагрузка;

·  моментная нагрузка – так представляется приложенная к конструкции пара сил.

Как правило, балки имеют те или иные опорные устройства – опоры. Конструктивные формы опор разнообразны. Для расчета их схематизируют в виде трех основных типов опор (рисунок 1):

а) шарнирно-подвижная опора (рисунок 1, а), в которой может возникать только одна составляющая реакции – ;

б) шарнирно-неподвижная опора (рисунок 1, б), в которой могут возникать две составляющие – вертикальная реакция  и горизонтальная реакция ;

в) защемление (жесткое защемление или заделка), где могут быть три составляющие – вертикальная  и горизонтальная  реакции и опорный момент  (рисунок 1, в).

Все реакции и моменты считаются приложенными в точке А – центре тяжести опорного сечения.

Балка, показанная на рисунок 2 а, называется простой, или однопролетной, или двухопорной, а расстояние  между опорами – пролетом.

Консолью называется балка, защемленная одним концом и не имеющая других опор (рисунок 2, б), или часть балки, свешивающаяся за опоры (рисунок 2, в, г). Балки, имеющие свешивающиеся части, называют консольными (рисунок 2, в, г).

Для рассмотрения равновесия произвольной плоской системы сил можно составить только три уравнения равновесия, из которых можно определить три неизвестные величины. Если число неизвестных равно числу уравнений равновесия, то такая задача является статически определимой. Если общее число неизвестных больше числа уравнений равновесия, то такая задача является статически неопределимой (рисунок 2, д).

Балки, имеющие опоры, в которых общее число неизвестных реакций равно числу уравнений равновесия, называются статически определимыми (рисунок 2, а, б, и, г).

Для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы алгебраическая сумма всех сил и алгебраическая сумма моментов всех сил относительно произвольной точки  равнялись нулю, т.е.

,          .

Возможна другая форма записи уравнений равновесия: для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы алгебраические суммы моментов всех сил относительно двух произвольных точек  и  равнялись нулю:

,        .

Правила составления уравнений равновесия для плоской системы параллельных сил:

1. Оси координат следует направлять так, чтобы одна из них оказалась параллельной силам, приложенным к балке.

2. Уравнения моментов нужно составлять относительно точки, лежащей на линии действия силы.

2.2. Методические указания к выполнению лабораторной работы № 1

Лабораторную работу № 1 рекомендуется выполнять в следующем порядке:

1.  Выделить тело, равновесие которого необходимо рассмотреть.

2.  Изобразить заданные силы.

3.  Освободить тело от связей, приложив соответствующие реакции. При этом необходимо убедиться, что данная задача является статически определимой – число неизвестных величин должно быть не более трех. Если на балку действует распределенная нагрузка, то для определения реакций ее заменяют равнодействующей, которая равна площади эпюры нагрузки и приложена в центре тяжести этой эпюры.

4.  Направить оси координат и выбрать моментные точки.

5.  Составить уравнения равновесия.

6.  Решить систему полученных уравнений равновесия относительно неизвестных величин.

7.  Произвести проверку. Для этого следует составить не применявшуюся при решении сумму моментов или проекций. Равенство нулю алгебраической суммы проекций или моментов подтвердит правильность решения задачи.

Варианты задания 1 лабораторной работы № 1 для студентов очной формы обучения выбираются по таблице 1 и таблице 2.

Примечание:   А – последняя цифра номера зачетной книжки;

В – предпоследняя цифра номера

Численные данные к заданию 1 лабораторной

работы № 1

Таблица 1.

А	Схема по табл. 2	В	, м	, м	, м	, м	, кН м	, кН	, кН/м
0	9	0	2,0	3,2	1,8	10	7	20	22
1	8	1	2,2	3,4	1,9	10	7	19	21
2	7	2	2,4	3,6	2,0	11	8	18	20
3	6	3	2,6	3,8	2,1	11	8	16	19
4	5	4	2,8	4,0	2,2	12	9	15	18

Окончание табл.1

Схемы к заданию 1 лабораторной работы № 1

Таблица 2.

Окончание табл. 2

Варианты задания 2 лабораторной работы № 1для студентов очной, очно-заочной и заочной форм обучения выбираются по таблице 3 и таблице 4.

Примечание:   А – последняя цифра номера зачетной книжки;

В – предпоследняя цифра номера

Численные данные к заданию 2 лабораторной работы № 1

Таблица 3.

А	Схема по табл. 4	В	, м	, м	, м	, кН м	, кН	, кН/м
0	0	0	1,0	1,9	3,0	10	8	10
1	1	1	1,1	1,8	3,0	9	8	10
2	2	2	1,2	1,7	3,0	8	14	12
3	3	3	1,3	2,6	4,0	7	14	12
4	4	4	1,4	2,5	4,0	6	12	10
5	5	5	1,5	2,4	4,0	12	12	10
6	6	6	1,9	3,0	4,5	11	11	8
7	7	7	1,8	2,9	4,5	10	11	8
8	8	8	1,7	2,8	4,0	9	10	15
9	9	9	1,6	2,7	4,0	8	10	15

Схемы к заданию 2 лабораторной работы № 1

Таблица 4.

2.3. Контрольные вопросы

1.  Сформулируйте цель работы

2.  Что такое расчетная схема объекта?

3.  Укажите геометрические признаки бруса, оболочки и массивного тела

4.  Что представляют собой сосредоточенная сила, распределенная нагрузка и момент?

5.  Чем можно уравновесить пару сил?

6.  Чему равен момент силы относительно точки?

7.  Когда момент силы относительно точки равен нулю?

8.  Что такое связь?

9.  Как направлена реакция связи?

10.  Сколько составляющих реакции возникает в шарнирно неподвижной опоре?

11.  Какой принцип используется для определения реакций связи?

12.  Сформулируйте условия равновесия плоской системы параллельных сил

13.  Сколько уравнений равновесия можно составить для плоской системы параллельных сил?

14.  В каком случае проекция силы на ось балки равна нулю?

3. ЛАБОРАТОРНАЯ РАБОТА № 2

Анализ внутренних силовых факторов в элементах конструкций

Цель работы: анализ внутренних силовых факторов, возникающих в элементах конструкций при заданных внешних воздействиях.

Исходными данными для выполнения лабораторной работы служат результаты выполнения лабораторной работы № 1.

Для заданных схем балок требуется:

1.  Используя метод сечения составить и решить (относительно внутренних силовых факторов) уравнения равновесия для всех внешних и внутренних сил, приложенных к рассматриваемой части бруса.

2.  Построить эпюры внутренних силовых факторов. Указать опасные сечения.

3.  Оформить отчет о выполнении лабораторной работы № 2.

3.1. Общие положения

В элементе конструкции, подверженном воздействию внешних нагрузок, возникают внутренние усилия (внутренние силовые факторы), оказывающие сопротивление внешним воздействиям.

Изгибом называется деформация элемента конструкции, связанная с искривлением его оси под действием внешних нагрузок. При изгибе в поперченных сечениях балок возникают два внутренних силовых фактора: изгибающий момент и поперечная сила .

Для определения внутренних силовых факторов, действующих в поперечных сечениях балок, применяется метод сечений, сущность которого заключается в мысленном рассечении балки на две части и рассмотрении равновесия одной части. Взаимодействие частей балки заменяется внутренними факторами.

Поперечная сила  в сечении равна алгебраической сумме проекций всех сил, а изгибающий момент  равен алгебраической сумме моментов всех сил, расположенных по одну сторону от сечения. Знаки действующих сил и моментов следует определять в соответствии с принятыми правилами (рисунок 3).

Рисунок 3. Знаки поперечных сил и изгибающих моментов

Необходимо научиться правильно определять равнодействующую силу и изгибающий момент от равномерно распределенной по длине балки нагрузки.

Для наглядного представления об изменении внутренних силовых факторов в сечениях по длине балки строят эпюры. Эпюра – графическое представление распределения внутренних силовых факторов по длине балки. Для построения эпюры балку разбивают на участки. Границами участков являются сечения, где приложены сосредоточенные усилия (сила, момент) или начинается и заканчивается распределенная нагрузка. Для каждой эпюры проводится ось эпюры, параллельная оси балки. Используя методом сечений на каждом участке, определяют внутренние силовые факторы.

Положительные значения поперечной силы  и изгибающего момента  откладываются выше оси эпюры, а отрицательные значения – ниже оси эпюры.

Построенную эпюру принято штриховать линиями, параллельными оси эпюры. На эпюрах для характерных ординат обязательно указывается их значения, в кружочке – знак.

Эпюры поперечных сил  и изгибающих моментов  обладают общими свойствами, которые могут быть использованы для проверки правильности их построения:

-  если на некотором участке балки отсутствует распределенная нагрузка, то эпюра  – прямая, параллельная оси абсцисс. Эпюра изгибающих моментов  на этом участке – наклонная прямая.

-  если на некотором участке балки имеется равномерно распределенная нагрузка, то эпюра  – наклонная прямая, а эпюра изгибающих моментов  – парабола, которая обращена выпуклостью «навстречу» нагрузке.

-  изгибающий момент достигает максимума или минимума в тех сечениях, где поперечная сила обращается в нуль (эпюра  пересекает ось эпюры).

-  если в сечении действует сосредоточенная сила, то на эпюре  в этом сечении происходит скачок, равный по величине приложенной силе.

-  если в сечении приложена сосредоточенная пара сил, эпюра изгибающих моментов  в этом сечении имеет скачок, равный моменту пары сил.

-   

3.2. Методические указания к выполнению лабораторной работы № 2

Выполнять лабораторную работу № 2 рекомендуется в следующем порядке:

1.  Разбить балку на участки. Нанести сечения на расчетную схему и пронумеровать их.

2.  На каждом участке провести сечение и, рассматривая равновесие отсеченной части балки (левой или правой), составить уравнения, выражающие поперечную силу  и изгибающий момент .

3.  Построить эпюры поперечных сил  и изгибающих моментов , сопровождая эти построения необходимыми расчетами. На всех эпюрах следует написать численные значения  и  на границах участков и в точках математического максимума с указанием размерности численных величин. В пределах каждой эпюры следует соблюдать один масштаб для откладываемых величин.

4.  Установить опасные сечения.

3.3. Контрольные вопросы

1.  Сформулируйте цель работы

2.  Перечислите внутренние силовые факторы, возникающие при изгибе балки

3.  В поперечных сечениях балки возникают только изгибающие моменты. Укажите вид изгиба

4.  Поясните суть метода сечений

5.  Изменится ли значение внутренних силовых факторов в зависимости от того, будут ли они вычислены по величинам внешних сил, расположенных слева от сечения или справа от него?

6.  Определите вид деформированного состояния бруса, если в его поперечных сечениях возникают поперечная сила  и изгибающий момент

7.  Что такое эпюра?

8.  Как устанавливаются границы участков, на которые разбивается балка при построении эпюр?

9.  Могут ли быть скачки на эпюре изгибающих моментов, если балка нагружена сосредоточенными силами и распределенной нагрузкой?

10.  В каком случае на эпюре поперечных сил появляются скачки?

11.  Как изменяется изгибающий момент на участках, нагруженных равномерно распределенной нагрузкой?

12.  Как установить опасное сечение балки?

4. ЛАБОРАТОРНАЯ РАБОТА № 3

Определение рациональных размеров поперечных сечений элементов конструкций

Цель работы: подбор различных вариантов сечений и выбор рационального, обеспечивающего наименьший вес элемента конструкции.

Исходными данными для выполнения лабораторной работы служат результаты выполнения лабораторной работы № 1 и № 2.

Для заданных схем балок требуется:

1.  Для каждой из балок по допускаемым напряжениям МПа подобрать размеры профилей поперечного сечения (рисунок 4).

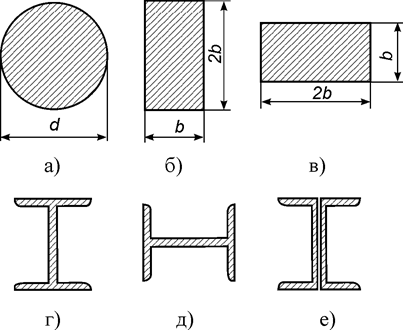
Рисунок 4. Профили поперечных сечений

2.  Для каждой балки по выбранным размерам поперечного сечения вычислить наибольшие нормальные напряжения и сопоставить их с допускаемыми нормальными напряжениями .

3.  Для балки с круглым (профиль а)) и прямоугольным (профили б)) поперечными сечениями вычислить наибольшие касательные напряжения  и сопоставить их с допускаемыми касательными напряжениями  МПа. Выполнить эпюру касательных напряжений.

4.  Выбрать рациональную форму поперечного сечения балки из условия минимального веса конструкции.

5.  Оформить отчет о выполнении лабораторной работы № 3.

Условия задания:

·  студенты очной формы обучения подбирают размеры всех поперечных сечений, представленных на рисунок 4;

·  студенты очно-заочной и заочной форм обучения подбирают размеры поперечных сечений а), б), в), г) из представленных на рис. 4.

4.1. Общие положения

Проверку прочности и подбор сечений балок, работающих на изгиб, производят исходя из следующих условий: наибольшие нормальные напряжения в поперечных сечениях не должны превосходить допускаемых напряжений, установленных нормами или опытом проектирования для материала балки.

Условие прочности имеет вид:

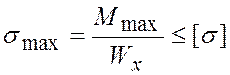.                                  (1)

Здесь  – наибольший по абсолютной величине изгибающий момент,  – наибольшие нормальные напряжения;  – момент сопротивления поперечного сечения.

Решая неравенство (1) относительно , получаем

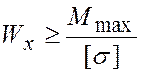.                                              (2)

По необходимому моменту сопротивления , задавшись формой сечения, подбирают его размеры.

Для круга диаметром :                  .

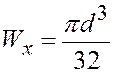Для прямоугольника :              .

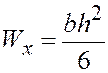Найденные размеры сечения следует округлять до ближайших стандартных, поэтому фактический момент сопротивления  может отличаться от расчетного . В результате напряжение в опасной точке будет отличаться от  и, следовательно, иметь место перенапряжение  или недонапряжение :

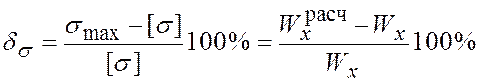.      (3)

При расчетах на прочность отклонение расчетных напряжений от допускаемых должно быть в пределах  величины допускаемых напряжений.

При поперечном изгибе, когда в поперечных сечениях балки действуют  и , возникают не только нормальные напряжения , но и касательные напряжения .

Касательные напряжения определяются по формуле Журавского. Наибольшей величины касательные напряжения достигают на нейтральной оси сечения и могут быть вычислены по формуле:

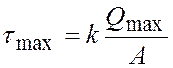.                                         (4)

Здесь  – наибольшая по абсолютной величине поперечная сила, установленная с помощью построения эпюры;  – площадь поперечного сечения;  – коэффициент, зависящий от формы сечения:

·  для прямоугольного поперечного сечения: ;

·  для круглого поперечного сечения; .

4.2. Методические указания к выполнению лабораторной работы № 3

Выполнять лабораторную работу № 3 рекомендуется в следующем порядке:

1. Определить необходимую величину момента сопротивления.

2. Задавшись формой сечения, подобрать его размеры. Полученные расчетом размеры поперечных сечений а), б), в) следует округлять до ближайшего значения по ГОСТ 6636-69 (Приложение 1). Для стандартных профилей г), д) размеры следует выбирать по таблицам ГОСТ 8239-89 (Приложение 2, таблица 6); размеры профилей е) – по таблицам ГОСТ 8240-89 (Приложение 3, таблица 7).

Для стандартных профилей (рисунок 4 г, д, е) брать ближайший профиль с большим моментом сопротивления.

3. Определить фактический момент сопротивления и величину .

4. Вычислить площадь  поперечного сечения для того, чтобы сравнить веса балок различных вариантов сечений, учитывая, что веса пропорциональны площади сечения.

Результаты рекомендуется представить в виде сводной таблицы, которая позволит судить о том, какие из полученных сечений рациональны для данной балки, а какие нет. Пример составления таблицы показан в таблице 5.

Сводная таблица результатов

Таблица 5. 

Сечение	, %	, см2	Относительный вес
Двутавр	9,2	26,8	1,0
Прямоугольник	0,2	79,4	2,96

Числа последнего столбика таблицы 5 показывают, во сколько раз балка с данным сечением тяжелее балки, вес которой