Фрикційні передачі. Кінематичні співвідношення у фрикційних передачах. Зубчасті передачі. Методи виготовлення зубчастих коліс. Види руйнування зубців, страница 5

2-й ряд: 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9;11;14;18;  22.

Окружність 1 (див. рис. 8.6), описана з центра колеса й обмежуюча вершини його голівок, називається окружністю вершин.

Окружність 2, описана з центра колеса й обмежуюча його западини з боку тіла колеса, називається окружністю западин.

Висотою зуба h називається радіальна відстань між окружністю виступів і окружністю западин.

Відповідно з ГОСТ 13755-68 висота голівки зуба приймається рівної модулю

.

Висота ніжки зуба приймається рівною 1,25 модуля

Висота зуба

.

Різниця у висоті ніжки зуба одного колеса і висоті голівки зуба іншого необхідна для утворення радіального зазору

.

Діаметр окружності виступів

d_a = d + 2h_a = zm + 2m = m (г + 2).

Діаметр  окружності  западин

d_f = d — 2h_f = zm — 2,5m = m (z — 2,5).

Модуль зачеплення можна визначити, знаючи діаметр окружності  виступів

.

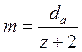Теоретична товщина зуба s і ширина западини s_з по ділильній окружності рівні між собою

.

Однак, щоб створити бічний зазор, необхідний для нормальної роботи зубцюватої пари, зуб робиться трохи тонше, унаслідок чого він входить у западину вільно.

Міжцентрова (міжосьова) відстань двох зачеплених зубчастих  коліс визначається  за формулою

.

Дугою зачеплення називають шлях, пройдений профілем зуба по початковій окружності за час фактичного його зачеплення. Дуга зачеплення позначається буквою S.

Необхідною умовою безперервності зачеплення є вимога,  щоб дуга зачеплення була більшою, ніж крок зачеплення, тобто щоб .

Відношення довжини дуги зачеплення до кроку зачеплення називається   коефіцієнтом  перекриття

.

Коефіцієнт перекриття характеризує середнє число пар зубців, що одночасно знаходяться в зачепленні. Для циліндричних зубчастих  передач  приймають .

8.4  Передаточне відношення серії зубчастих коліс.

У тому випадку, коли ведучий і ведений вали знаходяться на значній відстані друг від друга, передача руху за допомогою тільки двох зубчастих коліс виявляється невигідною, тому що габарити передачі виходять великими (рис. 8.7). Передачу з необхідним передатним відношенням доцільніше здійснити так, як показано на рис. 8.7, тобто  за допомогою декількох зубчастих коліс, насаджених на паралельні вали. На ведучий вал насаджене зубчасте колесо з діаметром d₁{ і числом зубців на ведений вал - колесо діаметром d₄ і числом зубів . Колеса з діаметрами d₂ і d₃ і числом зубців  і , що мають той же шаг,   називають проміжними або  «паразитними».

Передатне  відношення  першої  пари

;

другої пари

;

третьої пари

.

Перемноживши передатні відношення, знайдемо:

.

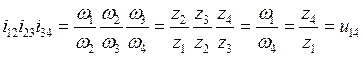Отриманий   результат   являє    собою   загальне    передатне   відношення   зубчастої   передачі.

З викладеного випливає, що загальне передатне відношення послідовного ряду зубчастих коліс із проміжними колесами дорівнює відношенню числа зубців веденого колеса до числа зубців ведучого.

Проміжні колеса не змінюють загального передатного відношення, але впливають на напрямок обертання веденого валу: при парному числі проміжних коліс напрямок обертання ведучого і веденого коліс протилежні, при непарному – однакові.

Включення серії малих зубчастих коліс замість двох коліс великих габаритів і маси при збереженні заданого передатного відношення знижує металоємність передачі, зменшує її габарити (що дуже важливо в машинах і верстатах) і дає можливість змінити напрямок обертання веденого колеса.

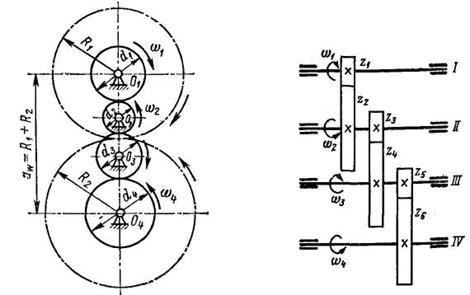
Рис. 8.7  Серія зубчастих коліс   Рис. 8.8  Багатоступінчаста передача

Однією парою зубчастих коліс неможливо здійснити передачу з великим передаточним відношенням (звичайно ). Для одержання великих передаточних відношень застосовують так називану багатоступінчасту передачу (рис. 8.8).

Передаточне число передачі

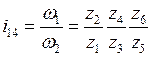
визначається  з наступних розумінь:

; ;  .

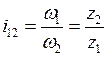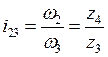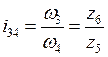Після перемножування цих  рівностей  одержимо

.

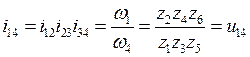Таким чином, загальне передатне відношення багатоступінчастої передачі дорівнює добуткові передаточних, відношень усіх ступіней.