Методичні вказівки до виконання курсової роботи з курсу “Взаємозамінність, стандартизація та технічні вимірювання”, страница 2

7. (Виконується тільки для перехідного сполучення) В перехідних посадках ступінь легкості складання та розбирання визначають імовірністю одержання у них зазорів чи натягів, (вираховують кількість з’єднань з натягом у відсотках від загальної кількості з’єднань).

Можна очікувати, що розподіл випадкових величин відхилень розмірів отвору та валу підпорядковується функції нормального розподілу (закону Гауса ). Визначимо з довірчою імовірністю +3s середнє квадратичне відхилення функції нормального розподілу для отвору та вала:

s_D = 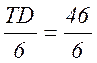 = 7,7 мкм,                 s_d = 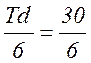 = 5 мкм.

Середнє квадратичне відхилення допуску посадки s_N визначаємо за формулою теорії імовірності:

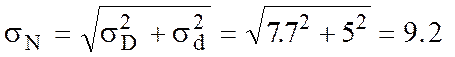мкм.

Центр групування кривої розподілу зазорів - натягів збігається з лінією середнього натягу, тобто відповідає найбільш ймовірним розмірам отвору та валу: М_(х) = N_c = 12 мкм.

Визначимо значення координати довірчого інтервалу розмірності середнє квадратичного відхилення s_N, який відповідає межі натягів та зазорів на графіку розсіювання зазорів (рис. 1.2):

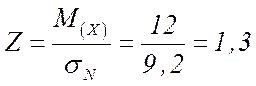
За табл. 1.3 знаходимо Ф (1,3) = 0,403.

Т.ч., відносна кількість з’єднань з натягом буде 0,5 + 0,403 = = 0,903 або 90,3%, з’єднань із зазором відповідно 9,7%.

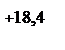
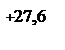
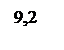
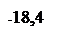
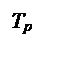
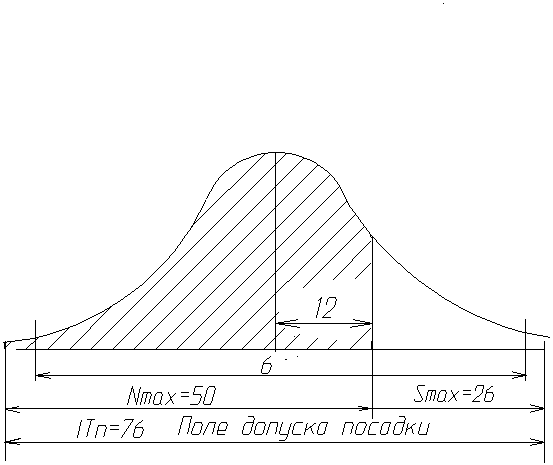
Рисунок 1.2 ‑ Графік розсіювання зазорів та натягів

з’єднання  63 H8/n7

Таблиця 1.3 ‑ Значення функцій Ф(t)

інтеграла ймовірностей (інтеграла Лапласа) в межах від 0 до + ¥