Уравнение неразрывности для несжимаемых жидкостей

где с — плотность жидкости, кг/м³; g_х, g_у,g_z — проекции ускорения поля внешних массовых сил на оси х, у, z, м/с²; р — давление, Па; м— динамическая вязкость, Па∙с; (* — коэффициент объемного расширения, 1/К; t_ж— температура среды (температура жидкости в ядре потока);

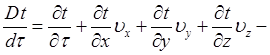субстанциальная производная;

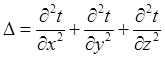оператор Лапласа.

С физической точки зрения уравнения (10.5) выражают равенство проекций равнодействующей всех сил, действующих на элемент объема жидкости (правые части уравнений), проекциям сил инерции (левые части уравнений). При этом первые слагаемые правых частей системы уравнений (10.5) выражают проекции подъемной силы, вторые слагаемые — проекции сил давления, третьи слагаемые — проекции сил внутреннего трения.

Уравнение неразрывности для несжимаемых жидкостей записывается в виде

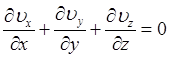                                                    (10.6)

Интегрирование системы уравнений (10.3), (10,5), (10.6) позволяет получить неизвестные функции t(х, у, г, ф), ( х, у, z, ф), р( х, у, z, ф). Для получения конкретного (частного) решения указанную систему уравнений необходимо дополнить условиями однозначности, которые, как и в случае интегрирования дифференциального уравнения теплопроводности (8.12), включают в себя геометрические, физические, начальные и граничные условия.

Геометрические условия определяют форму и размеры поверхности, обтекаемой жидкостью. Физические условия заключаются в задании значений физических величин жидкости, существенных для рассматриваемого процесса (плотности, вязкости, теплопроводности, теплоемкости, коэффициента объемного расширения). Граничные условия состоят в задании значений скорости и температуры жидкости у поверхности обтекаемой стенки и в ядре потока. У поверхности стенки обычно принимают скорость потока, равную нулю: продольные составляющие скорости по условию прилипания, а нормальная составляющая вследствие непроницаемости поверхности стенки. Температура жидкости t= t_с — у поверхности тела (стенки); t = t_ж— в невозмущенном потоке (в ядре потока жидкости), где t_c,  t_ж— соответственно температура стенки и среды (жидкости) вдали от стенки. Для установившихся режимов течения начальные условия не задаются.

Получив решение системы уравнений (10.3) при заданных условиях однозначности, можно рассчитать далее коэффициент

120