видно, что в этом случае свободный для пробега молекул объем будет равен х–b. Из-за уменьшения длины пробега молекул число ударов их о стенку в единицу времени (т. е. давление) увеличится в х/(х–b)раз. Иными словами,
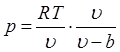
Силы притяжения между молекулами
приводят к возникновению молекулярного давления (в реальном газе из-за силы притяжения скорость
движения молекулы к стенке снижается, а следовательно, импульс силы удара о стенку
уменьшается). Сила молекулярного притяжения пропорциональна квадрату числа молекул,
приходящихся на 1 м2 поверхности, т. е. квадрату плотности, и
обратно пропорциональна удельному объему:
, где а —
коэффициент пропорциональности, зависящий от
природы реального газа.
Отсюда следует, что уравнение Ван-дер-Ваальса примет вид
(p+a/υ2) {υ—b) = RT. (1.8)
Уравнение (1.8) не всегда согласуется с опытом, что объясняется наличием в реальных газах отдельных групп, состоящих из двух, трех и более молекул.
На основе разработанной теории ассоциации молекул водяного пара М. П. Вукаловичем и И.И. Новиковым получено уравнение состояния, а также составлены таблицы и диаграммы свойств водяного пара, которые используют на практике для выполнения теплотехнических расчетов.
1.5. ГАЗОВЫЕ СМЕСИ
Смесь идеальных газов, химически не взаимодействующих между собой, называется идеальной газовой смесью. В соответствии с законом Дальтона
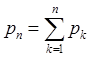
(1.9)
где рп — давление смеси; рk— парциальное давление k -го компонента смеси, равное давлению, которое имел бы данный компонент, если он занимал бы весь объем при температуре смеси; п — число компонентов смеси.
Уравнение состояния для k-гo компонента смеси имеет вид
(1.10)
а для смеси газов
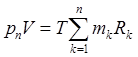
(1.11)
где тk— масса k-го компонента; Rk, — газовая постоянная k-го компонента. 10
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
