Измерение сопротивления постоянному току: Методические указания к выполнению лабораторной работы по курсу “Радиотехнические измерения”, страница 2

  Среднее значение  представляет собой результат усреднения ряда чисел, но не дает информации об их разбросе. Для этих целей вводят понятие стандартного отклонения, которое для последовательности X_i определяется выражением

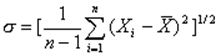      (7)

  Приведенная формула (7) показывает ширину распределения ошибок отдельных измерений. Здесь целесообразно проверить наличие в группе измерений грубых ошибок, учитывая, что при нормальном законе распределения ни одна случайная погрешность с вероятностью практически равной единице не должна выйти за пределы . Измерения, содержащие грубые погрешности, исключают из группы измерений и заново повторяют вычисления и s.

  Значение s  является случайной величиной. Это проявляется в том, что при повторении несколько раз серий из n измерений каждый раз будут получаться различные значения s. Поэтому следует провести оценку среднего арифметического значения стандартного отклонения

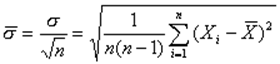        (8)

  При числе измерений n< 20 оценка доверительной границы случайной погрешности результата измерения вычисляется с учетом коэффициента Стьюдента t. Для n = 10 и доверительной вероятности Р = 0,99 коэффициент t = 3,25. 

  Таким образом, результат измерения следует записывать в виде

      , P     (9)

  Погрешность результата прямого однократного измерения оценивается до его выполнения и включает в себя погрешность средства измерения, погрешность метода и др. Все составляющие погрешности учитываются на основе анализа информации, полученной из опыта проведения подобных измерений, из технической документации и других источников. Однако распространены прямые однократные измерения в нормальных условиях, при которых всеми погрешностями, кроме инструментальной, пренебрегают. Анализ составляющих погрешностей таких измерений не проводится, а результат измерения записывается в виде

         (10) где А - показание средства измерения; D - абсолютная погрешность, определяемая классом точности измерительного прибора.

 Под классом точности понимают обобщенную характеристику точности средств измерений, определяемую пределами допускаемой основной погрешности. При этом пределы допускаемых погрешностей нормируют и выражают в форме абсолютных, приведенных или относительных погрешностей.

 Если класс точности К определен на основе приведенной погрешности, то пределы допускаемой абсолютной погрешности рассчитывают по формуле

       (11)

где D есть рабочий диапазон измерения. Само обозначение класса точности наносится на шкалу или корпус прибора в виде числа, например, 1,5. Если при этом шкала средства измерения существенно неравномерна, то под числом ставят галочку .

 Если класс точности определен на основе относительной  погрешности d, то пределы допускаемой абсолютной погрешности рассчитывают по формуле

           (12), а само число класса точности обводят кружком .

 В ряде случаев допустимо считать, что абсолютная погрешность измерения не хуже, чем половина цены деления шкалы средства измерения.

  При косвенном измерении результаты, полученные прямыми измерениями, являются исходными данными для дальнейших вычислений. Погрешности прямых измерений приводят к тому, что окончательный результат также имеет погрешности.

  Если искомая величина Х является некоторой функцией других величин Y_i, измеряемых прямыми методами, и они связаны между собой расчетной формулой

         (13)

то погрешность D этой величины определяется выражением

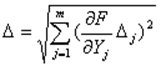       (14)

где D_j  - абсолютные погрешности в определении величин Y_j ;  - частные производные функции F по аргументу Y_j .