



























уровень безработицы среди цветного, а ![]() —
среди белого населения. Указанное соотношение выражает всего лишь тенденцию и
определяет линейную модель связи между рассматриваемыми
переменными.
—
среди белого населения. Указанное соотношение выражает всего лишь тенденцию и
определяет линейную модель связи между рассматриваемыми
переменными.
В нашем примере вычислим параметры, которые вычислили
в первой задаче, заметим при этом, что ![]() ,
,
![]() ,
, ![]() .
.
Запишем линейную модель наблюдений в виде
![]()
Для
оценки параметров α и β необходимо вычислить неизвестное значение дисперсии ![]() . Несмещенная оценка для
. Несмещенная оценка для ![]() является статистика
является статистика
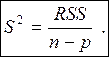
Получаем:
![]()
![]() =
=![]() . Коэффициент β
. Коэффициент β![]() оценивается величиной
оценивается величиной 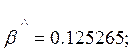 дисперсия
дисперсия 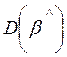 оценивается
величиной
оценивается
величиной ![]() . Для построения
. Для построения ![]() — доверительного интервала для β остается
найти квантиль уровня
— доверительного интервала для β остается
найти квантиль уровня ![]() распределения
Стьюдента с
распределения
Стьюдента с ![]() степенями свободы. Используя
справочник находим квантиль
степенями свободы. Используя
справочник находим квантиль ![]() .
Соответственно, получаем
.
Соответственно, получаем ![]() -доверительный
интервал для β в виде
-доверительный
интервал для β в виде
![]()
т. е.
![]()
Для
α имеем оценку ![]() ,
, ![]() ;
; ![]() -доверительный
интервал для α имеет вид
-доверительный
интервал для α имеет вид
![]()
т. е.
![]()
В связи с этим примером, отметим два обстоятельства.
(а) Доверительный интервал для коэффициента β допускает как положительные, так иотрицательные значения этого коэффициента.
(б)
Каждый из двух построенных интервалов имеет уровень доверия ![]() ; однако это не означает, что с той же
вероятностью
; однако это не означает, что с той же
вероятностью ![]() сразу оба
интервала накрывают истинные значения параметров α и β.
сразу оба
интервала накрывают истинные значения параметров α и β.
Справиться с первым затруднением в данном примере
можно, понизив уровень доверия до ![]() .
В этом случае в выражении для доверительного интервала квантиль
.
В этом случае в выражении для доверительного интервала квантиль ![]() заменяется на квантиль
заменяется на квантиль ![]() , так что левая граница доверительного
интервала для β становится положительной и равной
, так что левая граница доверительного
интервала для β становится положительной и равной ![]() . Однако это достигается ценой того,
что новый доверительный интервал будет накрывать истинное значение параметра
. Однако это достигается ценой того,
что новый доверительный интервал будет накрывать истинное значение параметра![]() в среднем только в 90 случаев из 100,
а не в 95 из100 случаев.
в среднем только в 90 случаев из 100,
а не в 95 из100 случаев.
Что касается второго затруднения, то наиболее простой путь взятия под контроль вероятности одновременного накрытия доверительными интервалами для α и β истинных значений этих параметров связан с тем, что
![]() оба интервала
накрывают α и β, соответственно
оба интервала
накрывают α и β, соответственно![]() =
=
![]() хотя бы один из
них не накрывает соответствующее
хотя бы один из
них не накрывает соответствующее ![]() =
=
![]() доверительный
интервал для α не накрывает α
доверительный
интервал для α не накрывает α![]() +
+
![]() доверительный
интервал для β не накрывает
доверительный
интервал для β не накрывает![]() β
β![]() -
-
![]() оба интервала
не накрывают свои
оба интервала
не накрывают свои ![]()
![]() =
=
![]()
![]() оба интервала не накрывают свои
оба интервала не накрывают свои![]()
![]() ³
³
![]()
Следовательно, если построить доверительный интервал
для α и доверительный интервал для β с уровнями доверия каждого, равными ![]() , то тогда правая часть полученной цепочки
соотношений будет равна
, то тогда правая часть полученной цепочки
соотношений будет равна ![]()
Это
означает, что в нашем примере мы можем гарантировать, что вероятность
одновременного накрытия истинных значений α и β соответствующими доверительными
интервалами будет не менее ![]() , если
возьмем
, если
возьмем ![]() . Но тогда при построении этих
интервалов придется использовать вместо значения
. Но тогда при построении этих
интервалов придется использовать вместо значения
![]()
значение
![]() ,
,
так
что каждый из исходных интервалов увеличится в ![]() раза.
раза.
Задача 6
Тема: Использование оцененной модели для прогнозирования
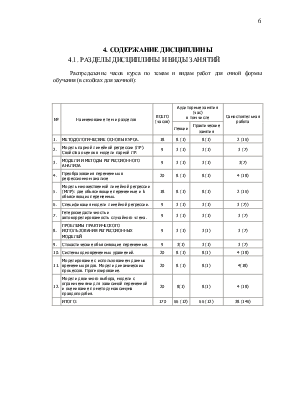
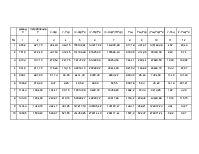
Исходные данные для этой задачи будут аналогичными данным о совокупном располагаемом доходе и совокупных личных расходах в некоторой стране в период с 1991 по 2000 год с поправками на инфляцию. Данные представлены в условных единицах, за основной год взят 1993 год — пересчет к последним выполнен с учетом динамики индекса потребительских цен в указанном периоде. (Уровень цен в 1993 г. принят за 100%.)
|
Год |
Потребление с учетом инфляции |
Доход с учетом инфляции |
|
1991 |
672,1 |
751.6 |
|
1992 |
696,8 |
779.2 |
|
1993 |
737,1 |
810.3 |
|
1994 |
767,9 |
864.7 |
|
1995 |
762,8 |
857.5 |
|
1996 |
779,4 |
874.5 |
|
1997 |
823,1 |
906.4 |
|
1998 |
864,3 |
942.9 |
|
1999 |
903,2 |
988.8 |
|
2000 |
927,6 |
1015.7 |
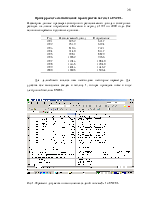
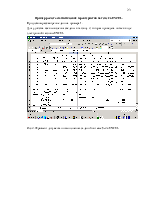
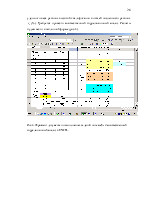
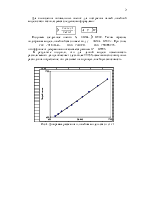
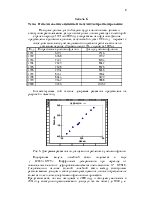
Соответствующая этой таблице диаграмма рассеяния представлена на рисунке 3 и имеет вид
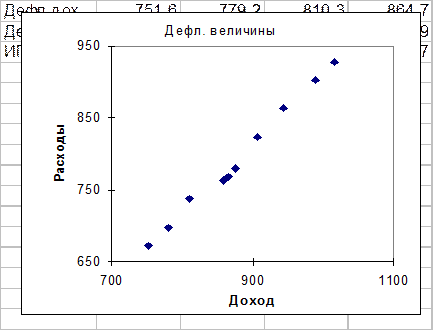
Рис. 6. Диаграмма рассеяния по доходам и потреблению с учетом инфляции
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.