Экономика и менеджмент \ Математические модели технологии работы железных дорог

Имитационное моделирование входящего на станцию поездопотока, страница 2

четвертый поезд считается прибывшим на станцию в 19-01.

Аналогичные расчеты проведем до конца суток, полученные результаты занесем в таблицу 1.

Моделирование категории поезда может производиться путем построения оси вероятностей и также с использованием таблицы случайных чисел. На рис. 2.1 показана ось вероятностей для случая, когда 45% грузовых поездов проходят сортировочную станцию без переформирования.

Рис. 2.1. Ось вероятностей для моделирования категории грузовых поездов

Поскольку случайные числа равномерно распределены в интервале,то при многократном повторении эксперимента около 45% чисел попадут в интервал от 0 до 0,45 и около 55% - в интервал от 0,45 до 1. Будем принимать последовательность случайных чисел из третьего столбца таблицы случайных чисел. Тогда

для первого поезда 0,8199>0,45, значит, поезд подлежит расформированию;

для второго поезда 0,1904<0,45, значит, поезд проходит станцию без переработки;

для третьего поезда 0,3279<0,45, поезд проходит станцию без переработки;

для четвертого: 0,5128>0,45, значит, поезд подлежит расформированию.

Аналогичные расчеты проведем для всех поездов в течение суток, результаты занесем в таблицу 1.

Моделирование направлений подхода грузовых поездов будем также производить путем построения оси вероятностей и также с использованием таблицы случайных чисел. На рис. 2.2 показана ось вероятностей для случая, когда 18% грузовых поездов проходят на сортировочную станцию с направления А, 22% - с направления Б, 28% - с направления В, 32% - с направления Г.

Рис.2.2. Ось вероятностей для моделирования направлений прибытия грузовых поездов.

Поскольку случайные числа равномерно распределены в интервале,то при многократном повторении эксперимента около 18% чисел попадут в интервал от 0 до 0,18, около 22% - в интервал от 0,18 до 0,40, около 28% в интервал от 0,4 до 0,68 и около 32% - в интервал от 0,68 до 1. Будем принимать последовательность случайных чисел по четвертому столбцу таблицы случайных чисел. Тогда

для первого поезда 0,18<0,3956<0,4, следовательно, поезд пришел с направления Б;

для второго поезда 0,8227>0,68, следовательно, поезд пришел с направления Г;

для третьего поезда 0,8368>0,68, следовательно, поезд пришел с направления Г

для четвертого поезда 0,7241>0,68, следовательно, поезд пришел с направления Г.

Аналогичные расчеты проведем для всех поездов в течение суток, результаты занесем в таблицу 1.

Известно, что число вагонов в составах грузовых поездов распределено по нормальному закону. Совокупность случайных чисел с заданным нормальным законом распределения получают особым способом, основанном на центральной предельной теореме теории вероятностей. Согласно ей при сложении достаточно большого числа независимых величин, сравнимых по дисперсиям, получается случайная величина, распределенная приближенно по нормальному закону. Опыт показывает, что случайная величина, которая с точностью, достаточной для большинства прикладных задач, может считаться нормальной, получается при сложении всего шести случайных чисел от 0 до 1. Значение такой случайной величины с математическим ожиданием и среднеквадратичным отклонением , определяют по формуле

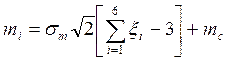. (2.2)

Рассчитаем число вагонов в грузовых поездах, принимая последовательность случайных чисел по пятому столбцу таблицы случайных чисел, с учетом того, что в нашем случае , :