Анализ многолетней динамики заболеваемости населения

Укрупнение периодов — применяется, когда явление в интервальном ряду выражено в абсолютных величинах, уровни которых суммируются по более крупным периодам. Применение возможно при кратном числе периодов

2. Вычисление групповой средней — применяется, когда уровни ряда выражены в абсолютных, средних или относительных величинах, которые суммируются, а затем делятся на число слагаемых. Способ применяется при кратном числе периодов.

3. Расчет скользящей средней — применяется, когда явление выражено в абсолютных, средних или относительных величинах. Каждый уровень заменяется на среднюю величину (из данного уровня и двух соседних с ним). Данный метод применяется, когда не требуется особой точности, когда имеется достаточно длинный ряд и можно пренебречь потерей двух значений ряда; в случаях, когда изучается развитие явления под влиянием одного или двух факторов.

4.  Метод наименьших квадратов применяется для более точной количественной оценки динамики изучаемого явления. Этим способом получаются такие выровненные значения уровней ряда, квадраты отклонения которых от истинных (эмпирических) показателей дают наименьшую сумму.

Количество функций, объединенных общим названием – методы наименьших квадратов, довольно разнообразно. Для ознакомления приведем наиболее часто встречаемые в практике эпидемиологического анализа методики:

а) выравнивание динамического ряда по функции параболы первого порядка (Y = a + bx), т.е. по прямой.

б) выравнивание динамического ряда по функции параболы второго порядка (Y = a + bx + cx²)  

в) выравнивание динамического ряда по функции параболы третьего порядка (Y=a+bX+cX²+dX³)

г) выравнивание динамического ряда по функции           экспоненциальной кривой (Y = ab^x)

д)выравнивание динамического ряда по функции степенной кривой (Y = аХ^ь)

Характерные типы кривых, используемых при выравнивании динамических рядов методом наименьших  квадратов, показаны на     рисунке 7.                                                                                           Рисунок 7        

Характерные  типы  кривых,  используемых  при  выравнивании  динамических  рядов

методом  наименьших  квадратов

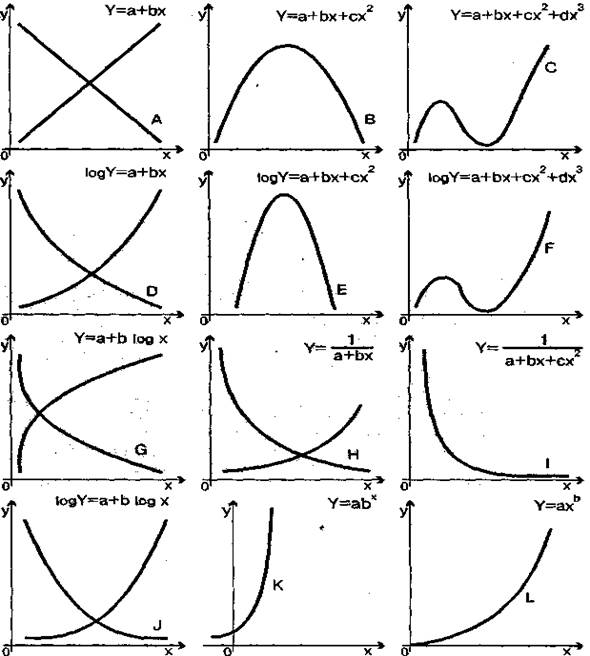
Примечание:Y – показатель заболеваемости;

                      а – коэффициент выражающий начальную скорость динамики;

            b, c, d – коэффициенты отражающие постоянную скорость тенденции во времени;

                      х – коэффициент нумерации лет согласно специальной схемы.

Выравнивание динамического ряда по функции параболы первого порядка (Y = a+bx).

         Наиболее информативное отражение многолетней заболеваемости – линейная диаграмма. Беглый взгляд на линейную диаграмму уже позволяет предположить имеющуюся тенденцию. Но для точной и наглядной характеристики производят расчеты, используя разные методы (функции). Метод выравнивание динамического ряда по параболе 1-го порядка (по прямой), является высоко информативным и позволяет определить коэффициент тенденции, его количественную характеристику, среднемноголетний (за анализируемый период) уровень заболеваемости.

1. Этапы расчета.

1.1. Составляем таблицу (с учетом выделенных границ периодов).

1.2. Расчет суммы (åу) заболеваемости (начиная с данного пункта все расчеты выполняются для каждого выделенного подпериода отдельно). Знак суммы (å) предполагает суммирование вариант по графам таблицы, соответственно.

1.3. Определяем интервалы (x):

а) если четное число анализируемых лет, то интервалы берутся через один от середины ряда.

Например: при n = 8 значения интервалов в графе "х" будут:

 –7; -5; -3; -1; 1; 3; 5; 7.

б) если нечетное число анализируемых лет, то значения "х" берутся по порядку от нуля с середины ряда.

Например: при n = 7 значения интервалов в графе "х" будут: