Основные принципы химии атмосферы, страница 3

   В атмосфере большое число газов взаимодействуют одновременно. Поэтому для определения времени жизни какой-либо компоненты следует анализировать все возможные про­цессы ее образования и гибели. Например, для следующего набора:

                             

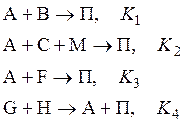
где П – продукты реакций, получаем:

            ,

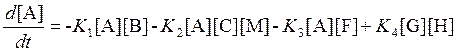откуда

                          .

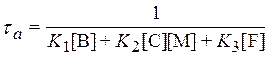Как видите, для оценки времени жизни учитываются только те процессы, которые приводят к разрушению молекулы А. Если это время малó относительно процессов переноса, и концентрации В, С, F, G, Н не меняются за это время, можно предположить существование фотохимического стационарного состояния (равновесия). Это значит, что , следовательно

                           .

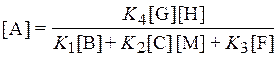Столкновительная теория бимолекулярных реакций

Простые представ­ления дают полезную схему для понимания реакции двух тел. Очевидно, что реакция А + В не может протекать со скоростью большей, чем ско­рость столкновения А и В. Представим, что частицы являются твердыми сферами. Тогда константа скорости столкновений между частицами  см³/с, где V_r - относительная скорость частиц, b - сечение столкновений: b =π(r_A+ r_B)². Для типичных молекул b - величина порядка  10^-15 см², а относительная скорость частиц в условиях, близких к термодинамическому равновесию,

                               ,

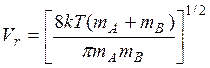где k - постоянная Больцмана, T - температура. Этот результат получен на основании распределения Максвелла для скоростей молекул газа, находящегося в термодинамическом равно­весии. Для типичных масс m_А, m_B средняя относительная скорость V_r – величина порядка 4·10⁴ см/с и К_ABимеет порядок величины 4∙10^-11см³/с. Видно также, что К_ав~ Т^1/2.

На самом деле реальное взаимодействие между реагирующими газами гораздо сложнее, и не все константы скорости бинарных реакций равны 4·10^-11см³/с. Точнее, для очень небольшого числа реакций получается такое значение константы. Причи­на - в ошибочности предположения, что частицы при столкновении ведут себя как твердые сферы.

В общем случае в ходе реакции частицы образуют промежуточные составляющие (их еще называют активированными комплексами). Грубо процесс представляется схемой, приведенной на рис.8.1

Для образования активированного комплекса необходима так называемая энер­гия активации Е_акт. Если реагирующие частицы обладают достаточной энергией, чтобы перейти барьер промежуточного комплекса, реакция произойдет, и образуют­ся продукты реакции.

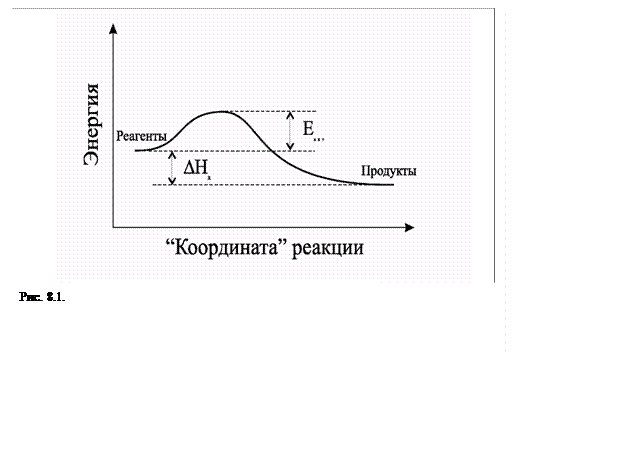Доля сталкивающихся частиц с энергией Е > Е_акт определяется согласно больцмановскому распределению - . Далее, даже если энергия столкновения достаточна для преодоления активационного барьера Е_акт, реакция может не произойти из-за неудачной ориентации сталкива­ющихся компонент. Поэтому следует ввести стерический фактор р, показывающий, какая часть общего числа соударений характеризуется «удобной» ориентацией. Тогда для К_авполучаем известную формулу Аррениуса[5]:

                                        .

В детальном изложении теория соударений более сложна, но, в конце концов, она приводит к выражению, подобному приведенному выше.

Еще один источник возможных ошибок в модели твердых сфер заключается в при­роде взаимодействия сталкивающихся частиц. Например, в случае ионно-молекулярных реакций между реагентами действуют электрические силы притяжения, и такие ре­акции должны идти быстрее, чем следует из простой теории столкновения твердых сфер.

Мономолекулярные реакции

Особый случай мономолекулярных реакций следует рассмотреть отдельно. Каков механизм распада молекулы на составные ча­сти? Ведь данный тип реакции, на первый взгляд,  нельзя понять на основе столкновительной теории бимолекулярных реакций.

В 1922 году Линдеманн (Frederick Alexander Lindemann, 1886-1957, – английский физик, советник по науке Уинстона Черчилля) выдвинул идею, впоследствии принятую учеными, что реакции, кажущиеся мономолекуляр­ными, в действительности являются итогом трех процессов

.

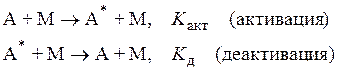
Скорость разрушения А:

                                    .

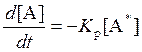Равновесная концентрация компоненты А* определяется из уравнения

                    .

Отсюда

                                                    .

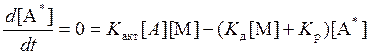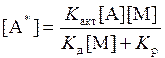Подставим в предыдущее соотношение, считая, что концентрация [А*] действительно всегда равновесная. Тогда получим