Физика зональной циркуляции атмосферы, страница 5

Довольно трудно доказать, что именно такова причина суперротации в случае атмосферы. Поэтому давайте попытаемся понять, в чем дело, на более простой модели. Представьте два диска, жестко закрепленных и вращающихся на оси с угловой скоростью Ω (рис. 18.5). Это будет примитивной моделью Земли. Вокруг дисков расположены тонкие кольца, движущиеся с относительными угловыми скоростями α₁<0 и  α₂>0 вокруг дисков. Между кольцами и дисками имеется трение. Поэтому, поскольку первое кольцо отстает, оно за счет трения забирает часть углового момента M₁ у дисков. Второе кольцо обгоняет диски и отдает за счет трения часть своего углового момента M₂ дискам.

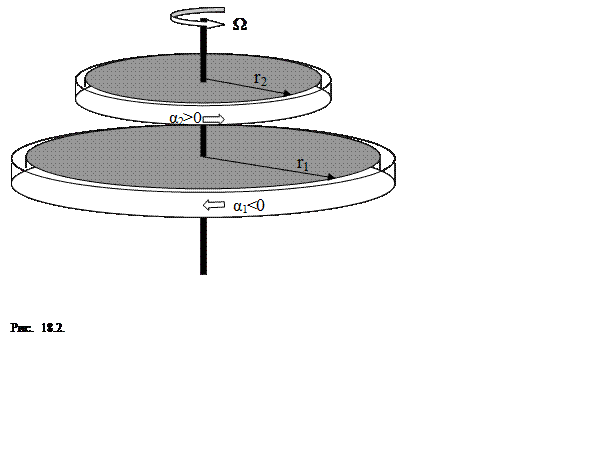
Предположим, что кольцо 1 с помощью какого-то механизма передает забираемый момент кольцу 2 так, что имеет место стационарное движение с постоянными  угловыми скоростями Ω, α₁, α₂. Нам здесь нет необходимости конкретизировать механизм обмена угловыми моментами между кольцами. Достаточно знать, что в атмосфере такой механизм существует и заключается в меридиональном обмене воздухом. Очевидно, что для баланса должно быть

                            .                                                                                         (18.1)

Рассчитаем суммарный относительный момент двух колец L:

                    .

В этой формуле ρ – линейная плотность колец (предполагается одинаковой). Забираемый момент определяется силой трения кольца 1 о диск 1. Сила трения F пропорциональна относительной скорости и длине контакта кольца с диском. Следовательно, момент силы трения

                              ,

где k – линейный коэффициент трения. Тогда, из условия баланса (18.1) имеем

                            или       .                                                    (18.2)

Как и следовало ожидать, , если .

Но это еще не суперротация, поскольку в рамках сделанных предположений суммарный относительный угловой момент обоих колец получается равным нулю. Нетрудно видеть, что положительный суммарный угловой момент (суперротация) получится, если, например, , то есть, сила трения зависит от скорости по степенному закону: F~V^β, β<1. Это весьма необычное предположение. Другой, более приемлемый вариант получается, когда коэффициенты трения для обоих колец различаются. В частности, для суперротации должно быть . Поскольку распределение суши и океана по земной поверхности неоднородно, такая версия выглядит весьма правдоподобной.

Наконец, антисуперротацию можно получить, предположив, что кольца имеют конечную толщину h<<r₁,r₂. Тогда для суммарного углового момента  можно приближенно записать, используя соотношение (18.2) для случая одинаковых коэффициентов трения

                .

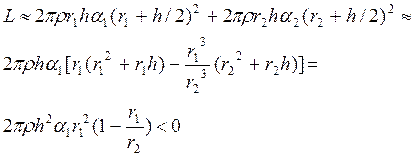Таким образом, нет ничего удивительного, что суммарный угловой момент атмосферы отличен от нуля. На примере нашей модели мы убедились, что в зависимости от небольших вариаций постановки задачи можно получать отсутствие супперотации, суперротацию и даже антисуперротацию. Удивительно и труднообъяснимо только то, что на самом деле относительный угловой момент атмосферы положителен. Для поиска причины (или нескольких причин) очевидно, нужны скрупулезные вычисления для более адекватной  модели атмосферы, чем была использована нами.

На первый взгляд, трудно смириться с ситуацией, когда относительный угловой момент атмосферы положителен в состоянии установившегося движения атмосферы. Казалось бы, Земля должна была бы все время получать дополнительный момент и раскручиваться все сильнее. Однако этого не происходит. Похожая ситуация имеет место и с нагревом Земли солнечным излучением. Представьте, что Солнце стало посылать на Землю в два раза больше энергии. Разве при этом баланс притока и оттока тепла нарушился бы настолько, что Земля стала бы перегреваться и расплавилась? Нет. Только в первое время (возможно, весьма продолжительное) температура Земли стала бы расти. Это происходило бы до тех пор, пока излучаемая в мировое пространство энергия (растущая с увеличением температуры пропорционально четвертой степени последней) не сравнялась бы с падающей. Опять наступило бы равновесие, только при более высокой температуре. Точно так же устанавливается равновесие между отбираемым атмосферой моментом импульса в экваториальной зоне и отдаваемым Земле в более высоких широтах. Условия же баланса определяются, в первую очередь, характеристиками трения воздуха о земную поверхность и скоростью меридионального обмена моментом импульса.