ВАРИАНТ 10
№ 1
Пусть P, Q и R – следующие высказывания:
P: Я умираю от жажды.
Q: Мой стакан пуст.
R: Сейчас три часа.
Запишите следующие высказывания как логические выражения:
Если я не умираю от жажды, то мой стакан не пуст.
Я умираю от жажды и мой стакан не пуст.
Если я умираю от жажды, то мой стакан пуст.
№ 2
Докажите высказывание методом математической индукции:
1´1! + 2´2! + ... + n´n! = (n+1)! – 1 для всех натуральных n.
№ 3
В качестве универсального множества выберем U = {p,q,r,s,t,u,v,w}.
Пусть A = {p,q,r,s}; B = {r,t,v}; C = {p,s,t,u}.
Найдите элементы следующих множеств:
а) BÇC
б) ![]()
в) AÈC
г) (AÈB)Ç(AÇC)
№ 4
Используя законы алгебры множеств докажите следующие тождества:
б) ![]() = AÈBÈC
= AÈBÈC
№ 5
Определите, какие отношения на ℤ (множестве целых чисел) являются рефлексивными, симметричными, а какие транзитивными?
а) «х+y – нечетное число»;
б) «x+y – четное число»;
в) «xy – нечетное число»;
г) «x+xy – четное число».
№ 6
Нарисуйте диаграмму Хассе для частично упорядоченных множеств:
Множество всех подмножеств в {a,b,c} с отношением «X – подмножество Y».
№ 7
Функции f: ℝ®ℝ и g: ℝ®ℝ заданы условием:
f
(x) = x2 и 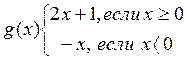 .
.
Выразите формулами композиции: f○g, g○f, g○g.
№ 8
Сколько разных «слов» можно получить из слова «АБРАКАДАБРА»? (по 11 букв каждое слово).
Сколько из них начинаются на «К»?
В скольких из них обе буквы «Б» стоят рядом?
№ 9
Матрица смежности орграфа G имеет вид:
М = 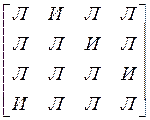
Вычислите М2, М3 и М4. Найдите матрицу достижимости M*.
№10
Найдите дизъюнктивную нормальную форму булевой функции f(p,q,r) c таблицей истинности
|
p |
q |
r |
f |
|
0 0 0 0 1 1 1 1 |
0 0 1 1 0 0 1 1 |
0 1 0 1 0 1 0 1 |
1 0 1 0 0 1 0 1 |
Изобразите карту Карно и упростите функцию f. Постройте ее функциональную схему.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.