


Санкт-Петербургский Государственный Политехнический Университет
Факультет Технической Кибернетики
Кафедра Автоматики и Вычислительной техники
ОТЧЕТ
Курсовая работа
Тема: Исследование осциллятора Ван дер Поля
Выполнила: студентка гр. 2081/4 Жданова Ю.
Проверил: Зимницкий В.А.
----
/подпись преподавателя, дата/
Санкт-Петербург
2009г.
Текст задания:
Задание N 19.
Исследование осциллятора Ван дер Поля (1 вариант).
Уравнение осциллятора имеет вид: ![]() .
.
Построить
графики U(t), ![]() для заданных начальных
значений:
для заданных начальных
значений:
U(0)
и ![]() , U(0)=A,
, U(0)=A, ![]() .
.
Значения
![]() задаются преподавателем.
задаются преподавателем.
Оценить погрешность результата и влияние на точность погрешности исходных данных. Рекомендуемое время наблюдения T=12 с. Шаг печати H=0.4 с.
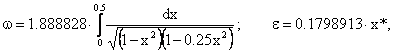 где x*- наименьший положительный
корень уравнения:
где x*- наименьший положительный
корень уравнения: ![]() . A=2;
B=0.
. A=2;
B=0.
Решение:
Задача решена в среде MatLab 7.0. Для нахождения ω решим интеграл с помощью программы QUADL. Для нахождения наименьшего положительного корня уравнения х=1.1х воспользуемся программой FZERO, где начальное приближение берём из графика:
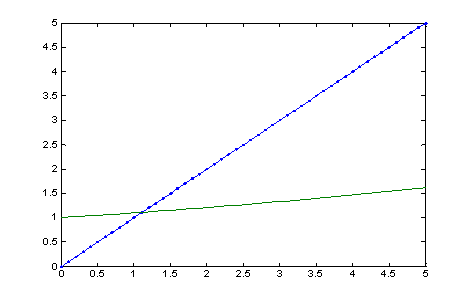
где прямая – 1.1х, а прямая с точками – х.
Для решения ![]() сделаем замену переменных:
сделаем замену переменных:
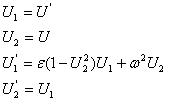
Решим теперь с помощью ODE45 систему дифференциальных уравнений.
Кодпрограммы:
Main
clear all;
format compact;
A = 2;
B = 0;
T = 12;
global e;
global w;
fun1=@(x) 1./( ( 1 - x.^2).*( 1 - 0.25*x.^2 ) ).^(1/2);
w = 1.888828*quadl(fun1, 0, 0.5)
fun2=@(y) y - 1.1.^y;
e = 0.1798913*fzero( fun2, 1 )
[t,U]=ode45( @fun3, [0,T], [B,A] );
plot( t, U(:,2) );
figure( 2 );
plot( U(:,2), U(:,1) );
fun3
function dUdt = fun3 ( t, U )
global w;
global e;
dUdt = [ e*(1 - U(2)^2)*U(1) - w.^2*U(2);
U(1) ];
Результат программы:
ω=1;
ε=0.2;
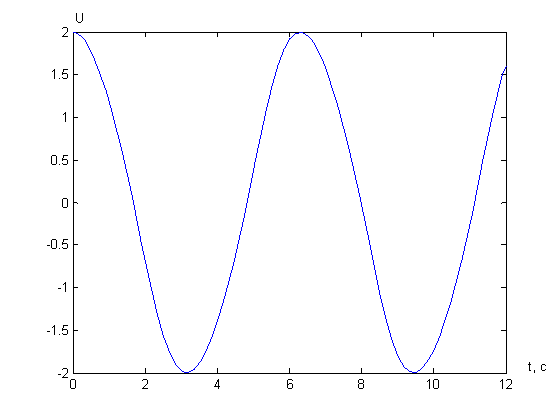
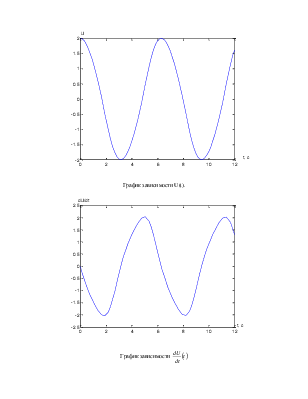
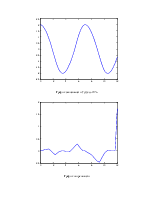
График зависимости U(t).
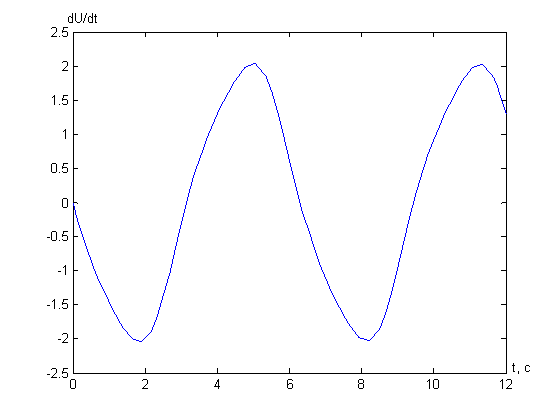
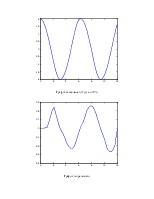
График зависимости ![]()
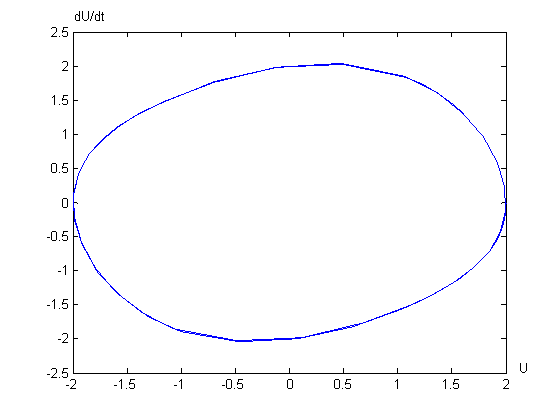
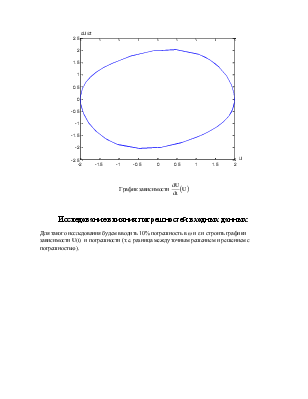
График зависимости ![]()
Исследование влияния погрешностей входных данных:
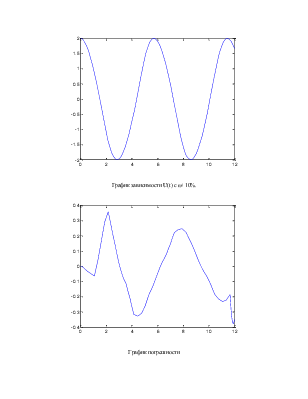
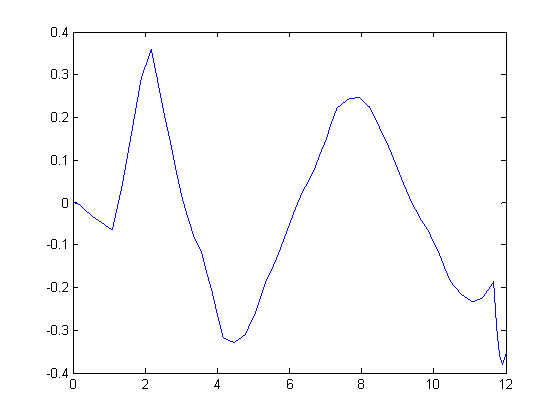
Для такого исследования будем вводить 10% погрешность в ω и ε и строить графики зависимости U(t) и погрешности (т.е. разница между точным решением и решением с погрешностью).
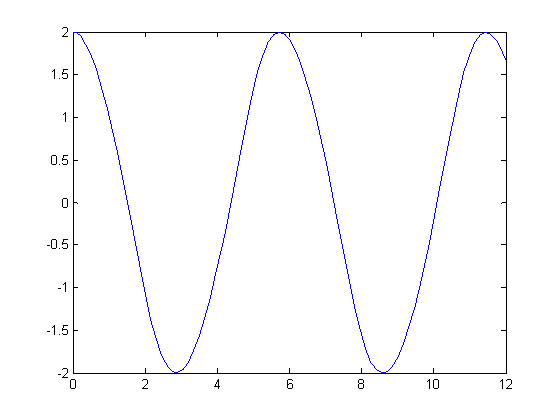
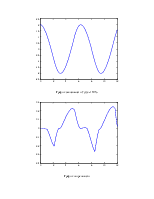
График зависимости U(t) с ω+10%.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.