Исследование осциллятора Ван дер Поля, страница 2

График погрешности

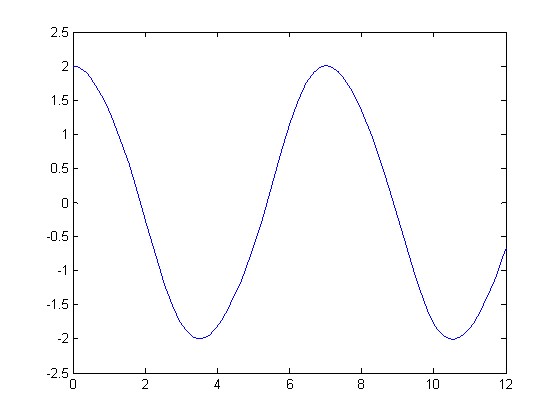
График зависимости U(t) с ω-10%.

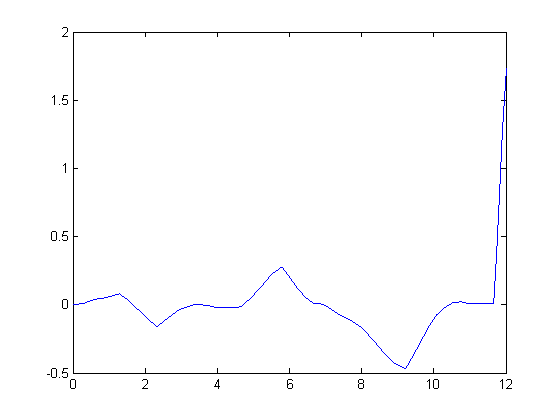
График погрешности

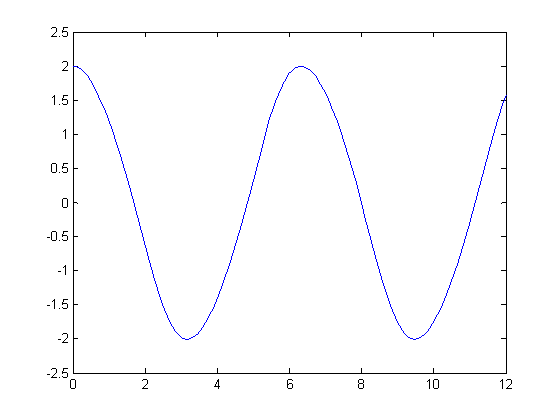
График зависимости U(t) с ε+10%.

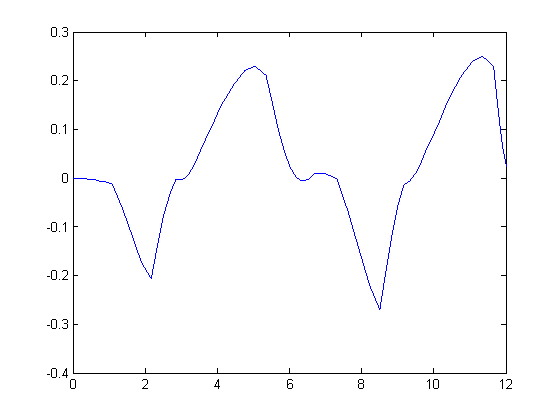
График погрешности

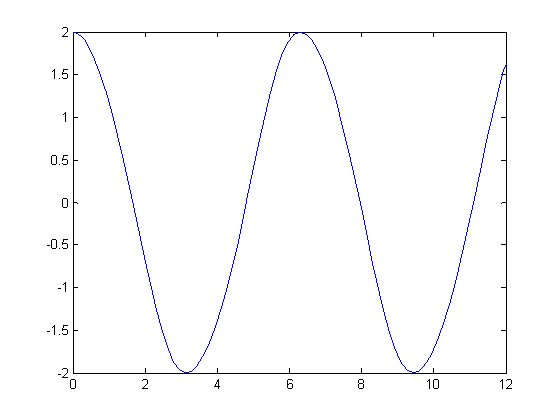
График зависимости U(t) с ε-10%.

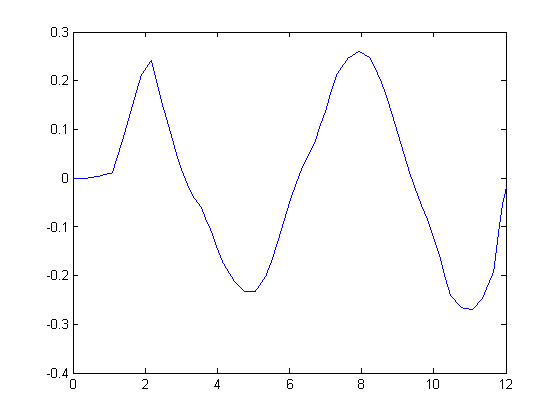
График погрешности

Вывод:

            В процессе выполнения получены графики зависимостей U(t) и . По этим графикам видно, что осциллятор Ван дер Поля совершает колебания, а второй график соответствует теории. Для оценки погрешности проанализируем код программы: для нахождения корня уравнения х=1.1^х использовали программу FZERO, которая считает нуль функции с погрешностью; для решения интеграла использовали программу QUADL, которая так же считает с погрешностью; для решения системы дифференциальных уравнений использовали ODE45, которая использует метод Рунге-Кутты 4, 5 степени точности, но так же имеет погрешность. Суммарная погрешность – есть сумма всех погрешностей, но так как они очень малы, то в целом можно считать, что полученные данные точны. После введения 10% погрешности в исходные данные, получили решение, которое отличается от точного. Большую погрешность вносит ω, т.к. происходит изменение периода колебаний.