Исследование тепловой проводимости и эффективной теплопроводности теплозащитной оболочки (Лабораторная работа № 7), страница 4

После завершения передачи данных контроллер готов к проведению следующего опыта.

Опыт № 2

Исследуется процесс нагрева медного образца в среде массивного дюралевого ядра с комнатной температурой. Образец окружен теплозащитной оболочкой, которая находится в хорошем тепловом контакте с массивным изотермическим ядром.

Целью опыта является определение проводимости K(Т) теплозащитной оболочки, которая играет в ячейке роль "постоянной" прибора в условиях нагрева образца в массивном изотермическом ядре.

При проведении этого опыта студент должен практически полностью повторить все основные операции предыдущего опыта (см. пункты 7…17). Для этого следует снова включить контроллер, сохранив в нем прежние установки, и быстро перенести тепловую ячейку из сосуда с азотом в сосуд с металлическим ядром.

После завершения опыта можно вынуть тепловую ячейку из дюралевого блока, вынуть из нее медный образец и удалить из него термопару.

С помощью контроллера передать всю информацию об опыте в базовый компьютер.

7.3. Расчетные формулы.

Пенопластовая оболочка, через которую в обоих опытах происходит теплообмен между медным стерженьком и изотермической средой (жидким азотом или водой), является достаточно тонкой и имеет очень малую массу (плотность пенопласта ~ 200 кг/м³), поэтому ее стенку можно упрощенно считать плоской, а теплоемкость пренебрежимо малой. Это позволяет считать, что температурное поле в поперечном сечении стенки остается в опыте условно стационарным и близким к линейному. Теплоемкость тонкостенной металлической трубки известна и учитывается, суммируясь с теплоемкостью медного стерженька.

В этих условиях для расчета эффективной теплопроводности материала ампулы может использоваться уравнение теплового баланса в системе "стерженек – стенка"

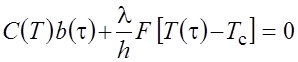,                            (7.3.1)

где С(Т) – суммарная теплоемкость стерженька и дюралевой трубкии при температуре Т; b(t) – изменяющаяся во времени скорость изменения температуры стерженька; l(Т, Т_с) – эффективная теплопроводность стенки ампулы; h – толщина стенки ампулы; F – активная поверхность стерженька, участвующая в теплообмене через стенку (без учета верхнего торца стерженька); Т(t) – изменяющаяся во времени температура стерженька; Т_с – температура изотермической среды (жидкий азот или вода).

Расчет эффективной теплопроводности воздушной прослойки может производиться по вытекающей из уравнения (7.3.1) формуле

.                           (7.3.2)

Для расчета эффективной тепловой проводимости оболочки пригодна формула

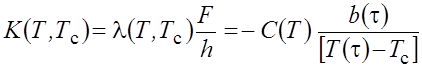.                  (7.3.3)

Для проведения необходимых расчетов по формулам (7.3.2), (7.3.3) следует осуществить детальную обработку полученных в опытах экспериментальных кривых Т(t). В частности, предстоит найти для каждой кривой Т(t) интерполяционный полином и продифференцировать его аналитически, чтобы получить затем полином для скорости изменения температуры стерженька b(t). Для реализации этих вычислительных процедур можно пользоваться стандартными компьютерными программами Excel и Origin 61. Их описание приведено в приложении.

Методика обработки обоих опытов остается общей. Не следует удивляться, если у полученных для эффективной теплопроводности расчетных кривых l(Т, Т_с) обнаружится систематическое расхождение, так как в данной работе измеряется теплопроводность, соответствующая значительным, изменяющимся во времени перепадам температуры в стенке ампулы.

В отчете следует привести первичные таблицы опытов и графики для эффективной теплопроводности и тепловой проводимости пенопластовой оболочки в условиях охлаждения и нагрева тепловой ячейки.