Транспонирование частоты при квантовании в компьютерных системах управления

Целью работы является изучение эффектов транспонирования частоты, возникающих при квантовании по времени сигналов, имеющих высокочастотную помеху.

2.  Методика проведения исследования

Под термином транспонирование частоты понимается преобразование сигнала из одного частотного спектра в другой. В частности при квантовании непрерывных сигналов по времени высокочастотный сигнал транспонируется в низкочастотный сигнал, что может существенно повлиять на поведение системы в целом.

При квантовании непрерывный сигнал представляется в виде некоторой решётчатой функции. Для квантования необходимо знать, при каких условиях он однозначно представляется своими дискретами. Ответ на этот вопрос даёт теорема Шеннона-Котельникова: «непрерывный сигнал, преобразование Фурье которого равно нулю вне интервала (-w₀, w₀), однозначно представляется своими значениями в равностоящих точках, если частота квантования больше 2w₀ (w_S = 2w₀, где w_S – частота квантования (рад/с), w₀ – максимальная частота сигнала, т. о. должно выполняться условие w_S > 2w₀). Квантование может быть как по времени, так и по уровню.

При квантовании по времени возникают амплитудные и частотные искажения. Если сигнал постоянный, то возникают только амплитудные искажения. Амплитудные искажения мы можем наблюдать, восстанавливая квантованный по времени сигнал фиксаторами. Частотные искажения можно разделить на фазовые, незначительно искажающие сигнал, и частотные, следствием которых имеют место явления транспонирования и поглощения частоты.

3.  Схема установки

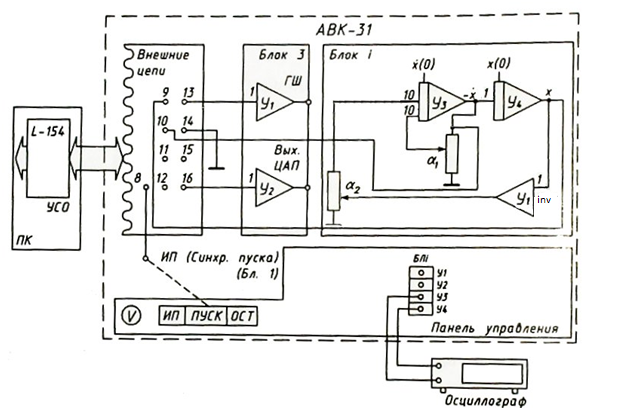
Рис. 3. Схема установки

4.  Выполнение работы

В ходе эксперимента на датчики с разной кратностью опроса подавался один и тот же гармонический сигнал с периодом . При этом

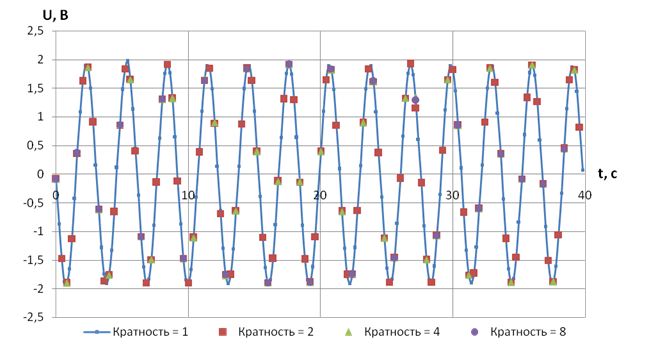
Рис. 4.1. Результаты опроса датчиков каналов с кратностями 1, 2, 4, 8

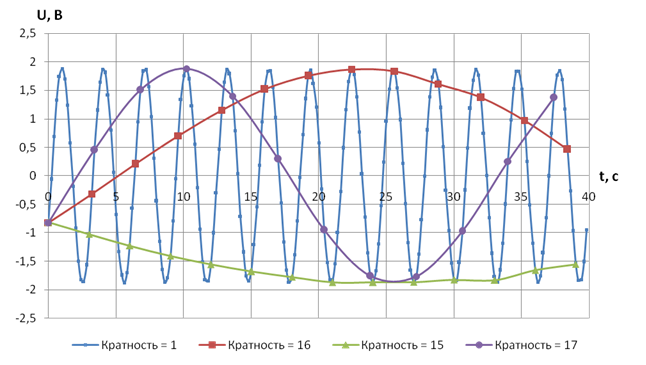
Рис. 4.2. Результаты опроса датчиков каналов с кратностями 1, 16, 15, 17

Выводы

В результате работы была экспериментально подтверждена возможность возникновения явления транспонирования частоты при нарушении условий теоремы Шеннона-Котельникова.

При первой серии измерений (рис. 4.1), где минимальная частота опроса датчиков в два раза выше собственной частоты сигнала, транспонирование частоты не происходит, и имеется возможность восстановить исходный сигнал.

При второй же серии измерений (рис. 4.2) выбрана частота опроса датчиков, близкая к собственной частоте сигнала. В данном случае наблюдается эффект транспонирования частоты. На выходе датчиков получается низкочастотный сигнал. Сигнал с датчика кратностью 16 представляет собой сверхнизкочастотный сигнал, так как при этом измерении частота опроса датчика совпадает с собственной частотой сигнала.