Математическое обеспечение. Нахождение корней уравнений. Аппроксимация функций. Численное интегрирование

ОСНОВЫ САПР.

Лекция 6. Математическое обеспечение

Содержание.

1. Основные численные методы.

2. Нахождение корней уравнений.

3. Аппроксимация функций.

4. Численное интегрирование.

5. Решение систем линейных уравнений.

Основные численные методы. Численные методы используются при разработке математических моделей большинства рассматриваемых задач.

1. Нахождение корней уравнений (метод деления отрезка пополам, метод Ньютона–Рафсона, др.)

2. Аппроксимация функций (кусочно-линейная, методом наименьших квадратов), интерполяция и экстраполяция функций.

3. Численное интегрирование функций (метод прямоугольников, трапеций, Симпсона и др.).

4. Решение систем линейных уравнений (метод Гаусса).

5. Решение систем нелинейных уравнений (метод Зейделя).

6. Решение дифференциальных уравнений и систем дифференциальных уравнений (метод конечных разностей).

7. Оптимизация.

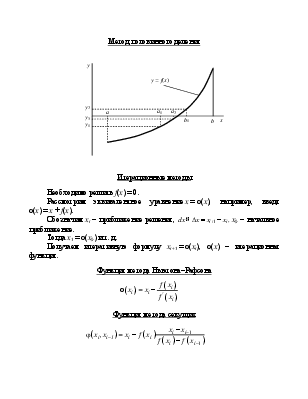
Нахождение корней уравнений.

Корень уравнения f(x) = 0

Если функция f(x) определена и непрерывна в интервале а < х < b, то корнем (нулем) функции f(x) называется такое значение аргумента х = х₀, при котором f(x) обращается в 0: f(x₀) = 0.

Алгоритм нахождения корней:

·  отделение корней;

·  уточнение приближенных корней.

Если непрерывная функция f(x) принимает значения разных знаков на концах отрезка [а, b], т. е.  f(a) · f(b) < 0, то внутри этого отрезка содержится, по меньшей мере, один корень уравнения f(x) = 0.

Метод половинного деления

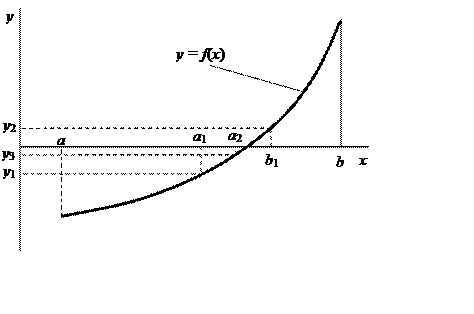Итерационные методы

Необходимо решить f(x) = 0.

Рассмотрим эквивалентное уравнение x = φ(x), например, введя φ(x) = x + f(x).

Обозначим x_i – приближение решения, , x₀ – начальное приближение.

Тогда x₁ = φ(x₀) и т. д.

Получаем итеративную формулу x_i+1 = φ(x_i), φ(x) – итерационная функция.

Функция метода Ньютона–Рафсона

Функция метода секущих

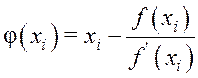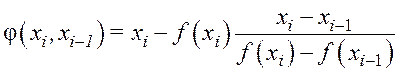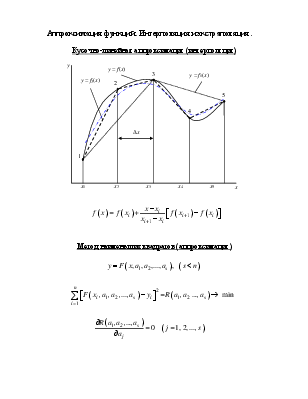
Аппроксимация функций. Интерполяция и экстраполяция.

Кусочно-линейная аппроксимация (интерполяция)

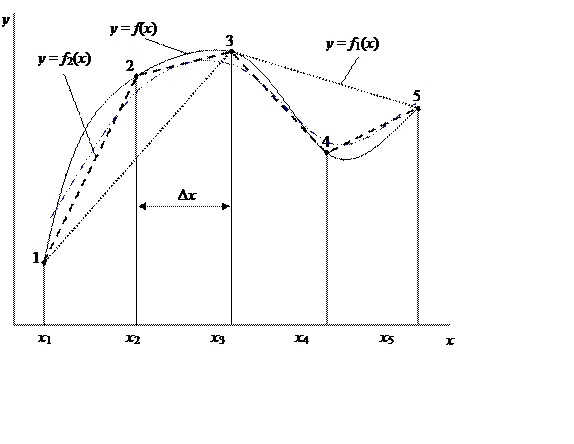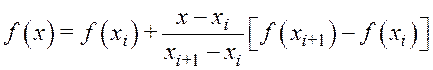Метод наименьших квадратов (аппроксимация)

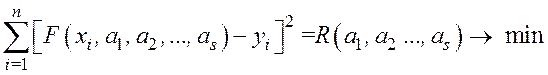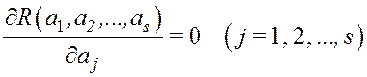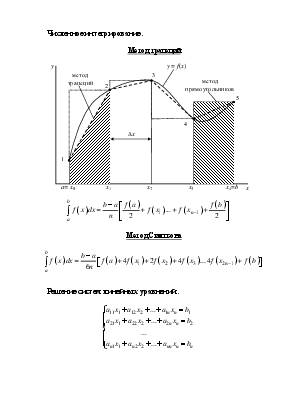
Численное интегрирование.

Метод трапеций

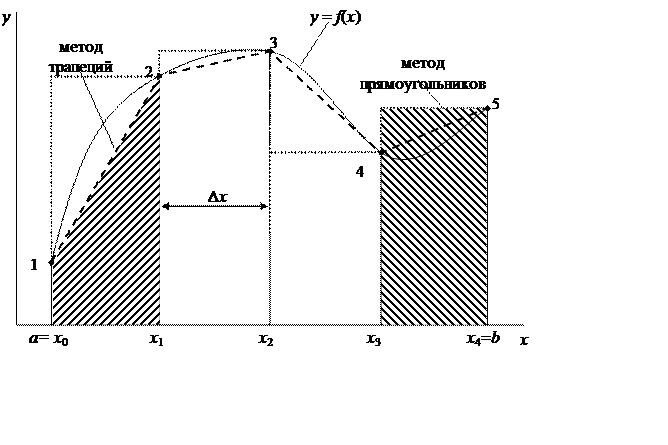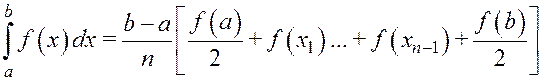Метод Симпсона

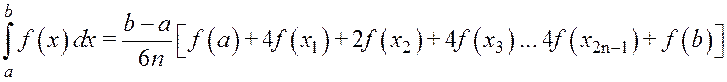Решение систем линейных уравнений.

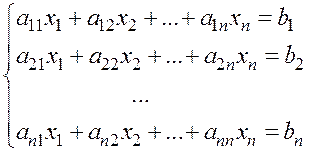Метод Гаусса (последовательных исключений неизвестных)

Метод основан на приведении матрицы коэффициентов  к треугольному виду. Алгоритм метода:

1.  С помощью двух циклов с управляющими переменными i = 1, 2, …, n  и  j = 1, 2, …, n организуем ввод коэффициентов  и b_i, образующих массивы.

2. 

Проводим прямой ход исключения переменных, путём преобразования коэффициентов по формулам

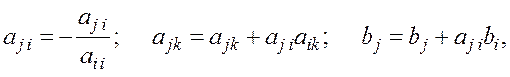где i = 1, 2, …, n – 1;      j = i + 1, i + 2, …, n;      k = k + 1, k + 2, …, n + 1

В конце этих преобразований получаем

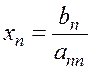3.   Организуем обратный ход (последовательное нахождение x_n–1, x_n–2, …, x₂, x₁)

,

где i = n – 1, n – 2, …, 2, 1;     j = i + 1, i + 2, …, n;     .

В результате формируется массив (вектор) неизвестных

.