 |

!П/п создания файла данных (2), загрузки созданного ранее файла (1)
!или вычисление значения по загруженному файлу (любое другое)
function apkl(ki,xi,ka)
common/fap/xx(20),yy(20,20)
allocatable x(:),y(:,:)
SELECTCASE (ka) !выбор варианта работы п/п
CASE (2) !создание файла
open(1,file='') !имя создаваемого файла данных
print*,'Zadaitenk'; read*,nk !количество функции
print*,'Zadaite ni'; read*,ni !кол-во значений по x
allocate(x(ni),y(nk,ni)) !динамическое выделение памяти
print*,'xi yi1 ... yik'
do i=1,ni;read*,x(i),(y(k,i),k=1,nk); enddo !ввод с клав.(<Tab>,<Enter>)
write(1,*)nk,ni !запись в файл
write(1,*)(x(i),i=1,ni) !запись в файл значений x
do k=1,nk; write(1,*)(y(k,i),i=1,ni); enddo!запись в файл значений y
close(1) !закрытие файла
pause 'file is created'
CASE (1) !загрузка файла
xx=0.; yy=0. !обнуление массивов в памяти
open(1,file='') !открытие существующего файла
read(1,*)nk,ni !чтение размерностей массивов
allocate(x(ni),y(nk,ni)) !динамическое выделение памяти
read(1,*)(x(i),i=1,ni) !чтение значений x
do k=1,nk;read(1,*)(y(k,i),i=1,ni);enddo !чтение значений y
do i=1,ni;xx(i)=x(i);do k=1,nk;yy(k,i)=y(k,i);enddo;enddo !в память
close(1) !закрытие файла
pause 'file is loaded'
CASEDEFAULT !вычисление функции
i=1; yki=yy(ki,1)
if(xi>xx(1))then
do while(xi>xx(i)); i=i+1; enddo
yki=yy(ki,i-1)+(yy(ki,i)-yy(ki,i-1))*(xi-xx(i-1))/(xx(i)-xx(i-1))
endif
apkl=yki
END SELECT
return
end
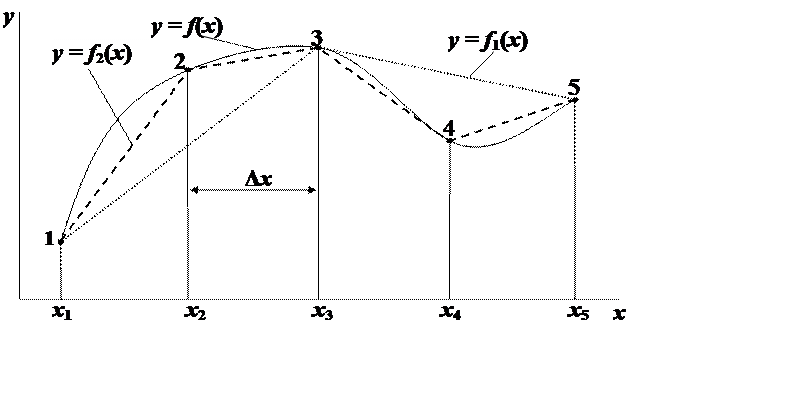
метод наименьших квадратов
y = F(x, a1, a2, …, as), (s < n)
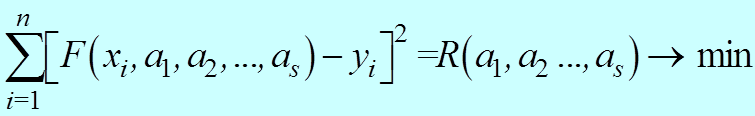
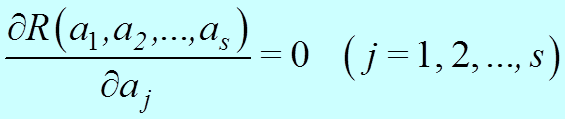
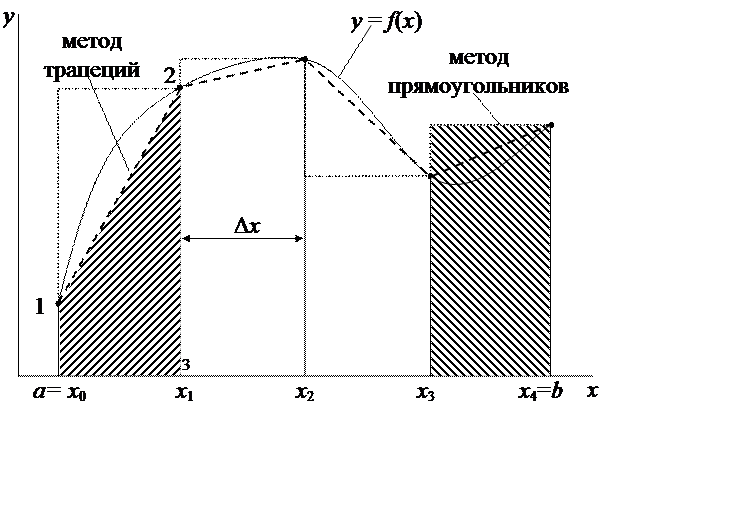 |
метод трапеций
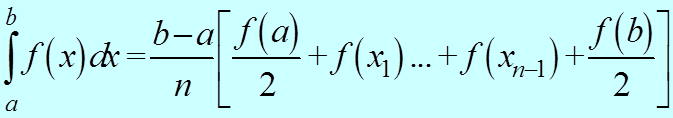
!МЕТОД ТРАПЕЦИЙ
!a,b-пределы интегрирования, f-подинтегральная функция
!Погрешность из условия, что уменьшение шага вдвое приводит
!к изменению результата на 0,01%
function fint(a,b,f)
external f
eps=1.; n=10;
s2=ss(a,b,n,f)
do while(eps>.0001)
s1=s2; n=n*2.;
s2=ss(a,b,n,f)
if(s2==s1)then; eps=0.
else; eps=abs(2.*(s2-s1)/(s1+s2))
endif; enddo
fint=s2
return; end
function ss(a,b,n,f)
external f
s=0.; h=(b-a)/n; x=a
метод Симпсона
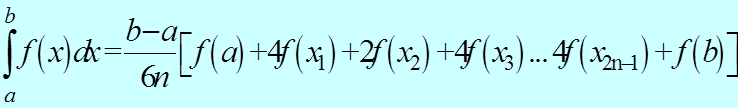
Решение систем линейных уравнений
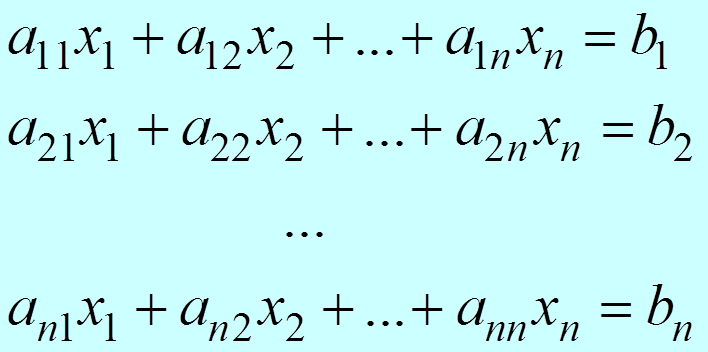 |
1.
Ввод ![]() и bi (i = 1, 2, …, n и j = 1, 2, …, n) в массивы a(i, j) и b(i).
и bi (i = 1, 2, …, n и j = 1, 2, …, n) в массивы a(i, j) и b(i).
2.
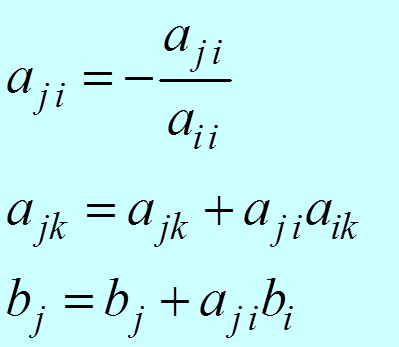 |
i = 1, 2, …, n – 1
j = j + 1, j + 2, …, n
k = k + 1, k + 2, …, n + 1
Получаем
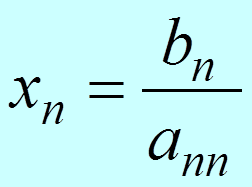 |
3. Обратный ход
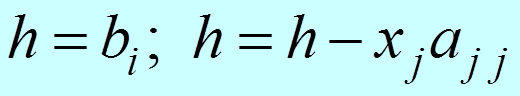 |
i = n – 1, n – 2, …, 2, 1
j = i + 1, i + 2, …, n
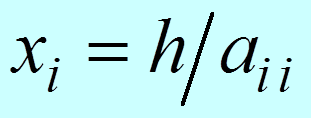 |
Результат
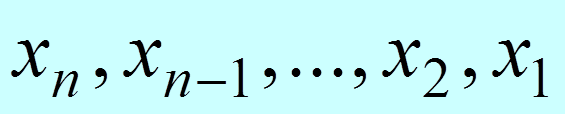 |

Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.