









МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ИСПОЛНИТЕЛЬНОГО
УСТРОЙСТВА КРИОТЕРАПЕВТИЧЕСКОГО КОМПЛЕКСА
Физическая модель ИУ КТК (см. 2.1) позволяет перейти к построению его математической модели.
Целесообразно исследовать процессы, протекающие в ИУ на
базе квазидвухмерной модели, интерпретирующей ИУ как единицу объема теплоносителя,
в которой присутствуют источники и приемники теплоты, и которая имеет конвективный
обмен массой с соседними полостями. При таком подходе можно вывести из
рассмотрения процессы, протекающие вдоль вертикальной координаты ![]() .
.
Через объем ИУ движутся два вида материальных потоков. Это поток теплоносителя от системы криостатирования в случае использования конвективного или смешанного способа отвода теплоты и потоку, поступающие через входные люки в момент перехода пациентов в объем ИУ и обратно. При понижении или повышении температуры газа в объеме ИУ возникает «компрессионный» поток в ОС.
 Схема движения тепловых и материальных потоков через
объем исполнительного устройства криотерапевтического комплекса поясняется рисунке
2.3.1. На схеме материальные потоки из смежного объема (шлюзовой камеры или ОС)
в объем ИУ – wj-1 и из объема ИУ в смежный
объем – wj условно
разнесены на разные стороны элементарного объема физической модели. В реальной
кабине эти потоки проходят через одну и ту же вертикальную плоскость, как
правило, через люк прохода пациентов. Поступление газа из смежного объема и
обратно оказывает существенное влияние на температуры теплоносителя в объеме
ИУ, поэтому этот вид материальных потоков подлежит обязательному
математическому описанию и анализу.
Схема движения тепловых и материальных потоков через
объем исполнительного устройства криотерапевтического комплекса поясняется рисунке
2.3.1. На схеме материальные потоки из смежного объема (шлюзовой камеры или ОС)
в объем ИУ – wj-1 и из объема ИУ в смежный
объем – wj условно
разнесены на разные стороны элементарного объема физической модели. В реальной
кабине эти потоки проходят через одну и ту же вертикальную плоскость, как
правило, через люк прохода пациентов. Поступление газа из смежного объема и
обратно оказывает существенное влияние на температуры теплоносителя в объеме
ИУ, поэтому этот вид материальных потоков подлежит обязательному
математическому описанию и анализу.
В многоместных КТК объем основной кабины и шлюза примерно равны между собой, поэтому при входе пациентов происходит перемешивание более теплого газа из шлюза с холодным газом кабины, в результате чего температура в объеме ИУ резко возрастает, а система криостатирования испытывает дополнительную тепловую нагрузку.
Конвективный перенос массы газа, связанный с работой системы криостатирования, рассматривается как движение вдоль координаты X. Материальные потоки, связанные с изменением плотности теплоносителя в объеме ИУ, рассматриваются как движение вдоль координаты Z.
Разделение материальных потоков по двум координатам – условный прием, направленный на упрощение анализа конвективного переноса теплоты при реализации рабочего цикла ИУ.
С учетом принятых допущений, уравнения энергии и неразрывности принимают более простой вид. Уравнение энергии связывает изменение энтальпии газа в элементарном объеме с подводом теплоты вдоль координат X и Z, а также от внутренних источников (приемников) теплоты:
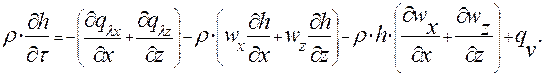 (2.3.1)
(2.3.1)
Уравнение неразрывности представляет собой материальный баланс элементарного объема:
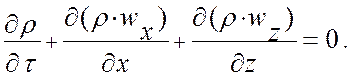 (2.3.2)
(2.3.2)
Исходя из особенностей физических условий, при которых протекает процесс ОКВ, можно еще упростить математическое описание технологического цикла КТК.
Учитывая то, что давление газа равно атмосферному, его теплопроводность мала, поэтому переносом теплоты теплопроводностью можно пренебречь:
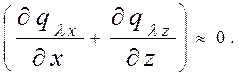
После исключения малозначительных составляющих уравнение энергии приобретает вид:
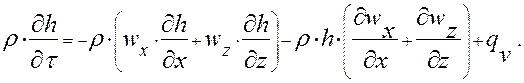 (2.3.3)
(2.3.3)
Из выражения 2.3.3 следует, что изменения энергии газа в объеме ИУ связаны с конвективным переносом теплоты по осям X и Z, c изменением плотности теплоносителя в объеме ИУ, а также с наличием распределенных источников (приемников) теплоты. Для упрощения построения математической модели можно представить уравнение (2.3.3) в виде теплового баланса единицы объема ИУ:
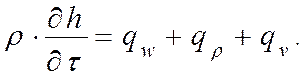 (2.3.4)
(2.3.4)
Изменения энтальпии
элементарного объема являются результатом подвода теплоты конвекцией ![]() , подвода теплоты за счет увеличения плотности
газа
, подвода теплоты за счет увеличения плотности
газа ![]() , теплоты подведенной от внутренних источников
, теплоты подведенной от внутренних источников
![]() .
.
Конвективный перенос теплоты возникает при использовании конвективного или смешанного способа отвода теплоты, а также при сообщении объема ИУ с соседними низкотемпературными полостями или окружающей средой через входные люки. Конвективный подвод теплоты к единице объема описывается выражением:
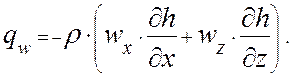 (2.3.5)
(2.3.5)
Ранее принято допущение, что перенос теплоты, связанный с работой системы криостатирования, рассматривается вдоль оси X:
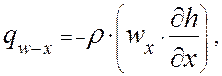 (2.3.6)
(2.3.6)
а тепловые потоки, связанные с проникновением газа из смежных полостей, направлены вдоль оси Z:
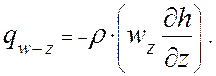 (2.3.7)
(2.3.7)
Такая дезинтеграция математической модели позволяет создавать
отдельные программные блоки, которые можно подключать или отключать при
моделировании частных процессов в ИУ. Например, в ИУ с рекуперативным охлаждением
(см. рисунок 2.3.1) нет подвода теплоты с потоком теплоносителя из системы
криостатирования, соответственно ![]() .
.
Подвод теплоты с потоком окружающей среды продолжается
в одноместном ИУ и длится не более 5 секунд. Все остальное время ![]() .
.
Рассуждая аналогично, запишем выражение для подвода теплоты, связанной с изменением плотности газа в объеме ИУ:
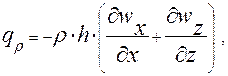 (2.3.8)
(2.3.8)
выражение для подвода теплоты за счет потока, поступающего от системы криостатирования:
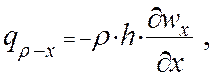 (2.3.9)
(2.3.9)
и потока подводимого из смежных полостей:
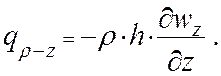 (2.3.10)
(2.3.10)
Существенное влияние на теплосодержание и температуру
теплоносителя оказывают внутренние источники (приемники теплоты). Наибольшее число
источников теплоты содержится в ИУ с рекуперативным охлаждением. В единице
объема ИУ находится часть теплопередающей поверхности объекта ОКВ ![]() , теплового ограждения
, теплового ограждения ![]() и теплообменного устройства
и теплообменного устройства![]() . Суммарный подвод теплоты от внутренних
источников составит:
. Суммарный подвод теплоты от внутренних
источников составит:
![]() ,
(2.3.11)
,
(2.3.11)
где, ![]() ,
, ![]() ,
, ![]() – плотность
теплового потока, отводимого теплоносителем с поверхности объекта ОКВ, от теплового
ограждения и от теплообменного устройства соответственно.
– плотность
теплового потока, отводимого теплоносителем с поверхности объекта ОКВ, от теплового
ограждения и от теплообменного устройства соответственно.
Тепловые потоки от источников (приемников) теплоты определяются разностью температур между их поверхностью и теплоносителем:
![]() (2.3.12)
(2.3.12)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.