Математическая модель исполнительного устройства криотерапевтического комплекса, страница 2

                                  (2.3.13)

                                 (2.3.14)

где, , ,  – температура поверхности теплоисточника (теплоприемника); , ,  – коэффициенты естественно-конвективной теплоотдачи от поверхностей объекта ОКВ, теплового ограждения и теплообменника соответственно. Величина коэффициента теплоотдачи зависит от температур теплоносителя и теплоисточника:

                                   (2.3.15)

                                    (2.3.16)

                                   (2.3.17)

Текущее значение температуры теплоносителя известно либо из начальных условий, если τ=0, либо из решения уравнения энергии на предыдущем временном слое, если τ>0.

Для расчета тепловых потоков от теплоисточников необходимы значения температуры их поверхности. Эти температуры могут быть определены только при использовании соответствующих математических моделей.

Математическая модель объекта ОКВ рассмотрена в 1.3.

Математические модели теплового ограждения и теплообменника необходимо разработать.

Построение математических моделей изоляции и теплообменника будет сделано позднее, а пока следует завершить формирование математической модели ИУ в части решения уравнения энергии.

Объем исполнительного устройства КТК сообщается с окружающей средой, поэтому давление теплоносителя постоянно и равно атмосферному. Колебания плотности теплоносителя связаны с изменением его температуры , которая колеблется в широких пределах. Колебания температуры теплоносителя в групповых ИУ связано с входом (выходом) пациентов в зону ОКВ, их амплитуда достигает 50-70К.

В индивидуальных КТК в момент входа (выхода) пациента объем ИУ заполняется атмосферным воздухом, такими образом дважды за цикл температура газа повышается до 150 К. Колебания температуры вызывают изменения плотности теплоносителя. Например, при заполнении индивидуального ИУ газом с номинальной температурой 140 К плотность теплоносителя меняется с исходных 1,172 до 2,42 кг/м³ [62].

Удвоение плотности приводит к тому, что часть поданного в объем ИУ теплоносителя не возвращается в систему криостатирования, а накапливается в объеме ИУ. В групповых КТК рост температуры теплоносителя при размещении в объеме ИУ пациентов, сопровождается повышением температуры, снижением плотности теплоносителя и сбросом части газа в смежную полость (шлюзовую камеру). После выхода пациентов, температура газа опускается до номинального уровня. При этом плотность теплоносителя растет, поэтому в объем кабины поступает воздух из смежной полости (шлюзовой кабины). Колебания плотности теплоносителя формируют один из источников подвода теплоты в объем ИУ .

Для учета колебаний плотности газа в единице объема ИУ используется уравнение неразрывности (2.3.2), которое представляет собой материальный баланс элементарного объема КТК:

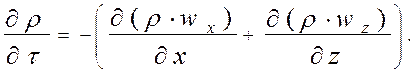             (2.3.18)

Применительно к моделированию работы ИУ криотерапевтического комплекса физический смысл уравнения неразрывности сводится к тому, что колебания плотности должны быть компенсированы подводом (отводом) газа вдоль одной из координат.

Вид уравнения неразрывности может изменяться в зависимости от способа криостатирования ИУ. В системах с рекуперативным криостатированием объема ИУ отсутствует перенос массы вдоль оси Х, т.е. . Тогда:

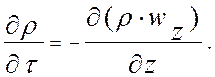                               (2.3.19)

При конвективном охлаждении исполнительного устройства подвод теплоносителя компенсирует колебания плотности, поэтому нет переноса массы вдоль оси Z и . При этом:

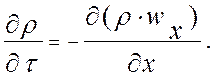                            (2.3.20)

Часть газа, поданного системой криостатирования, остается в объеме ИУ и не возвращается в СК.

При использовании схемы смешанного криостатирования объема ИУ следует использовать уравнение неразрывности в форме (2.3.19), так как отвод паров криоагента из зоны криостатирования осуществляется в соседнюю полость (шлюзовую камеру). Ранее было принято, что перенос теплоты в соседние объемы происходит по оси Z.

Моделирование процессов переноса теплоты и массы в ИУ КТК основано на численном решении системы уравнений энергии и неразрывности. В 1.3 рассмотрено решение уравнения энергии для твердого тела методом замены производных разностными приближениями. Используя этот метод, преобразуем выражения (2.3.5-8).

Перенос теплоты, связанный с работой системы криостатирования, рассматривается вдоль оси X:

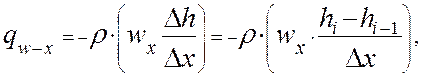                (2.3.21)

где,  – энтальпия теплоносителя на входе в объем ИУ и на выходе в систему криостатирования соответственно.

Подвод теплоты с газом из смежных полостей:

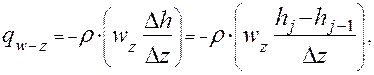                    (2.3.22)

где,  – энтальпия теплоносителя в смежной полости и в ИУ соответственно.

Интенсивность подвода теплоты при изменении плотности газа в объеме ИУ с потоком от системы криостатирования:

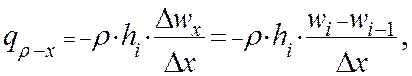              (2.3.23)

где,  – скорость теплоносителя на входе в объем ИУ и на выходе в систему криостатирования.

Интенсивность подвода теплоты при изменении плотности газа в объеме ИУ с потоком газа из смежных полостей:

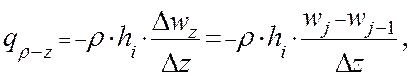               (2.3.24)

где,  – скорость теплоносителя на границе смежной полости и ИУ.

Значения энтальпии и скорости газа на границах ИУ определяют условия однозначности, которые отражают специфические особенности частных вариантов реализации КТК, поэтому условия однозначности целесообразно определять для каждой серии численных экспериментов.

Путем замены производных разностными приближениями приводим выражение (2.3.4) к следующему виду:

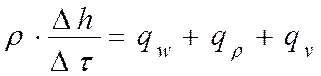                      (2.3.25)

или

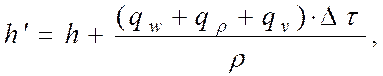              (2.3.26)

где  – энтальпия теплоносителя в момент времени τ+∆τ;  – подвод теплоты конвекцией, за счет изменения плотности, от внутренних источников соответственно.

                                  (2.3.27)

                                    (2.3.28)

                                (2.3.29)

В представленном виде математическая модель элементарного объема ИУ пригодна для разработки программного обеспечения. Для завершения формирования математического аппарата необходимы математические модели теплового ограждения и теплообменного устройства.