








перемещениях учитывают только деформации тела шпинделя и его опор. Собственные деформации обрабатываемой заготовки, оснастки, инструмента и различных соединений со шпинделем во внимание не принимают, относя их к самостоятельным задачам исследований. Оценке подлежит жесткость в радиальном и осевом направлениях.
10.2.1. Радиальная жесткость
Определение радиальной жесткости шпиндельного узла сводится к вычислению прогиба переднего конца шпинделя под действием нагрузок. При этом все силы раскладывают на составляющие в двух взаимно перпендикулярных плоскостях Y и Z, проходящих через ось шпинделя.
Формализация геометрических параметров
С целью упрощения расчетов шпиндель можно представить в виде балки постоянного поперечного сечения с моментом инерции, вычисляемым по формуле 10,4 [12, стр.86]:
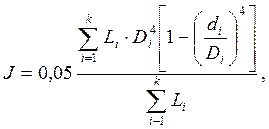 (10.4)
(10.4)
где Di и Li – соответственно наружный диаметр и длина отдельных ступеней; di – диаметр отверстий ступеней шпинделя.
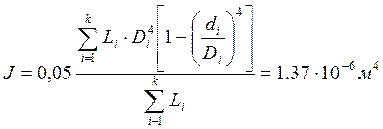
Определение направления и места приложения внешних сил
Эту задачу обычно решают путем построения единой пространственной схемы нагружения, исходя из условий работы ШУ. Она дает полную картину силового воздействия. В качестве исходных при этом используют такие ее частные компоненты, как конструктивная схема, схемы резания (рис. 10.1) и сил (рис. 10.2).
Наиболее типовыми условиями нагружения является сочетание силы резания с усилием в ременной или зубчатой передаче.
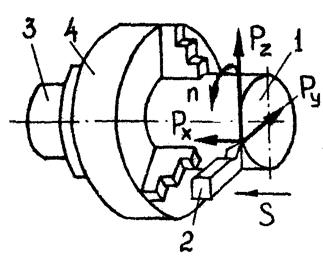
Рис. 10. 1. Схема резания при точении: 1 – деталь; 2 – инструмент; 3 – шпиндель; 4 - патрон
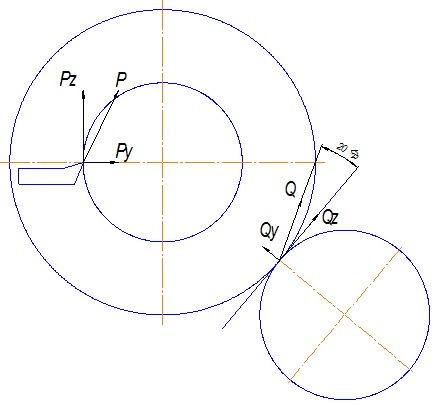
Рис. 10. 2. Схема сил на шпинделе: 1 – резец; 2 – деталь; 3, 4 – зубчатое колесо и шестерня
Наличие в передней опоре группы подшипников создает защемляющий момент m, который препятствует свободному проворачиванию шпинделя, со знаком, противоположным знаку нагрузки. С учетом этого, при переходе от реальных опор к идеализированным их заменяем их на упругие шарнирные с радиальной жесткостью jrA и jrB. При переносе силы Р в требуемое сечение на конце балки появляется дополнительно изгибающий момент М.
Момент на шпинделе поределяется по формуле 10,5:
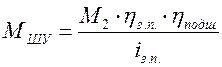 (10.5)
(10.5)
МШУ = 250 Н·м.
Главная составляющая силы резания определяется по формуле 10,6:
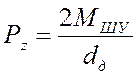 , (10.6)
, (10.6)
где dд = Dmax/2 = 200 мм – диаметр детали;
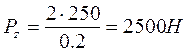
Радиальная составляющая силы резания определяется по формуле 10.7:
Рy = (0,3…0,5)Рz, (10.7)
Рy = (0,3…0,5)Рz =0,3×Рz = 0,3×2500 = 750 Н;
![]()
Величину координаты приложения силы h определяем из выражения 10.8:
![]() , (10.8)
, (10.8)
![]() - длина детали,
- длина детали,
![]() - толщина диска патрона.
- толщина диска патрона.
![]() .
.
Усилие в зубчатом зацеплении определяется по формуле 10.9:
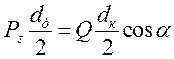 ; (10.9)
; (10.9)
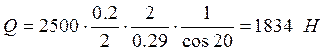
![]()
![]()
Составление расчетной схемы и определение активных и реактивных сил.
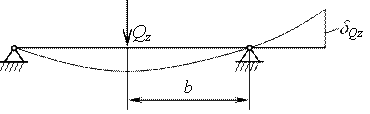
На рисунке 10. 3 и рисунке 10. 4 показаны расчетные схемы шпинделя для плоскости ZOX и YOX.
Так как нас интересует деформация переднего конца, то при переносе силы Р в требуемое сечение на конце балки появляется дополнительно изгибающий момент М.
Для определения величины прогиба удобно использовать принцип суперпозиции, согласно которому она складывается из суммы частных смещений балки от элементарных независимых нагрузок без учета жесткости опор и смещения абсолютно жесткой балки за счет податливости опор.
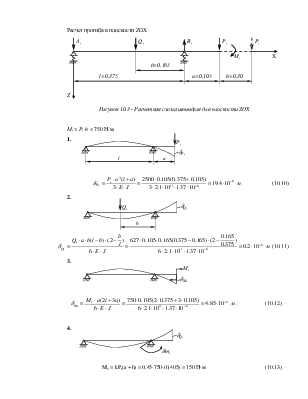
Расчет прогиба в плоскости ZOX
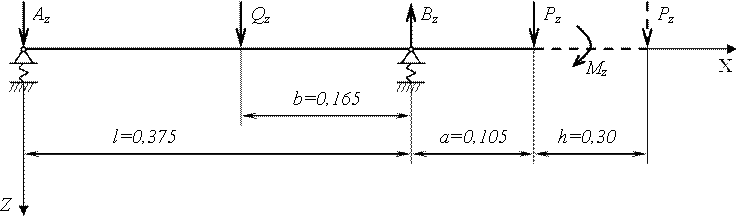 |
Рисунок 10.3 - Расчетная схема шпинделя для плоскости ZOX
 Мz
= Pz×h = 750 Н×м.
Мz
= Pz×h = 750 Н×м.
1.
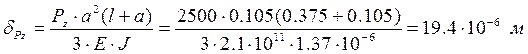 (10.10)
(10.10)
 2.
2.
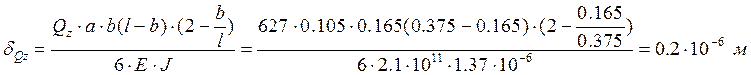 (10.11)
(10.11)
 3.
3.
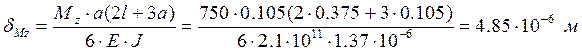 . (10.12)
. (10.12)
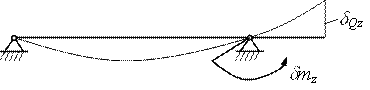 4.
4.
Mz = kPz(a +h) = 0,45×750×(0,405) = 150 Н×м (10.13)
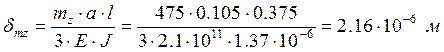 (10.13)
(10.13)
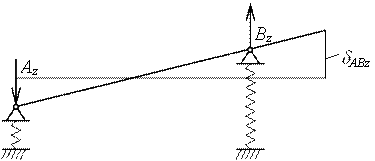
реактивный момент определим по формуле 10.15:
![]() (10.15)
(10.15)
 k – коэффициент
защемления (k=0,3…0,45).
k – коэффициент
защемления (k=0,3…0,45).
5.
Реакции опор определим по формулам 10.16 и 10.17 соответственно:
SМА = 0, – Рz×0,480 – Qz×0,21 + Bz×0,375 – Мz = 0, Bz = 4848 H; (10.16)
SМB = 0, – Рz×0,105 + Qz×0,165 + Az×0,375 – Mz = 0, Az = 2976 H; (10.17)
Жесткость определим по формуле 10.18:
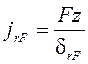 ,
(10.18)
,
(10.18)
где F – радиальное усилие, действующее на опору; z – количество подшипников, несущих нагрузку; drF – упругое смещение опоры определим по формуле 10.19:;
drF = d¢rF + d²rF, (10.19)
где d¢rF – упругие сближения тел качения и колец подшипника 10.20; d²rF – контактные деформации на поверхности посадки колец на шпиндель и в корпус 10.21;
d¢rF = К1×Fn; (10.20)
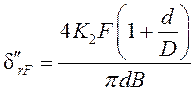 ,
(10.21)
,
(10.21)
где n – показатель степени (n = 1,0 для роликовых подшипников); d и D – соответственно внутренний и наружный диаметр подшипника; К1 и К2 – коэффициенты податливости находим по формуле 10.22:
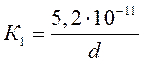 (для роликовых конических
подшипников), (10.22)
(для роликовых конических
подшипников), (10.22)
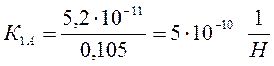 ,
,
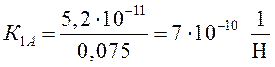 ;
;
d¢rАz = 7×10-10×2976 = 2,08×10-6 м,
d¢rВz = 5×10-10×4848 = 2,4×10-6 м;
К2 = 0,2×10-11 м3/Н,
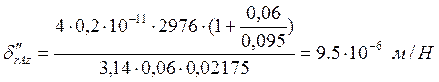 ,
,
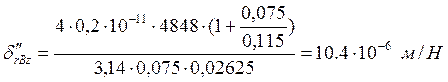 ;
;
Упругие смещения:
drАz = 2,08×10-6 + 9,5×10-6 = 11,58×10-6 м,
drВz = 2,4×10-6 + 10,4×10-6 = 12,8×10-6 м;
Жесткость:
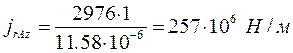 ,
,
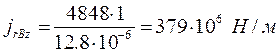 .
.
Прогиб dАВ конца шпинделя определяется по формуле
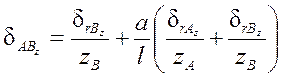 (5.17)
(5.17)
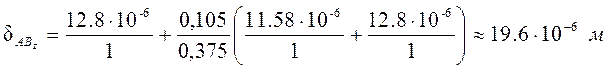
Уравнение прогиба конца шпинделя записывается в виде
drz
= dРz – dQz + dMz – dAвz -![]() = 1,94×10-5 – 0,02×10-5 + 0,485×10-5 –1,96×10-6 -0,216×10-6
=
= 1,94×10-5 – 0,02×10-5 + 0,485×10-5 –1,96×10-6 -0,216×10-6
=
= 2,3×10-6 м. (5.18)
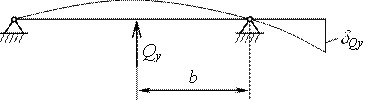
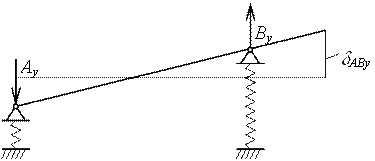
Расчет прогиба в плоскости YOX
 |
Рисунок 5. 4 Расчетная схема шпинделя для плоскости YOX
Мy = Py×h = 225 Н×м.
 |
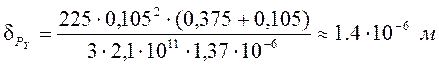 . (5.19)
. (5.19)
 |
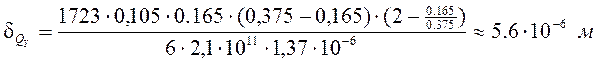 .
.
 |
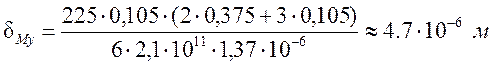 . (5.20)
. (5.20)
4.
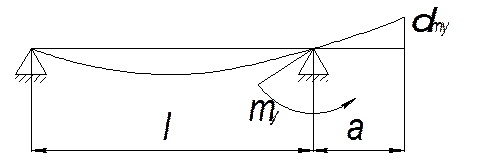
mу = kPy(a +h) = 0,45×750×(0,405) = 136,7 Н×м, (5.21)
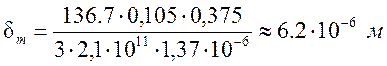 .
.
 5.
5.
определение реакций опор
SМА = 0, – Рy×0,480 – Qy×0,21 + By×0,375 – Мy = 0, By = 2525 H;
SМB = 0, – Рy×0,105 + Qy×0,165 + Ay×0,375 – My = 0, Ay = 52 H;
определение жесткости
d¢rАy = 5×10-10×52 = 2,6×10-8 м,
d¢rВy = 7×10-10×2525 = 1,76×10-6 м;
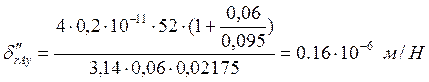 ,
,
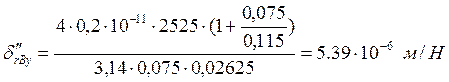 ;
;
Упругие смещения:
drAy = 2,6×10-8 + 0,16×10-6 = 0,186×10-6 м,
drВy = 1,76×10-6 + 5,39×10-6 = 7,15×10-6 м;
Жесткость:
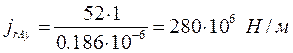
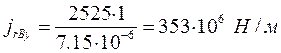 .
.
Прогиб dАВ конца шпинделя определяется по формуле
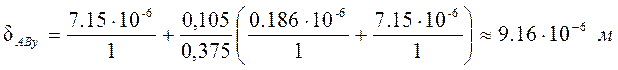 . (5.22)
. (5.22)
Уравнение прогиба конца шпинделя определим по формуле 5.23
dry = dРy + dQy +
dMy – dABy -![]() = 1,4×10-6 + 5,6×10-6 + 4,7×10-6 – 9,16×10-6 -6,2·10-6
= -3,66 ×10-6 м.
(5.23)
= 1,4×10-6 + 5,6×10-6 + 4,7×10-6 – 9,16×10-6 -6,2·10-6
= -3,66 ×10-6 м.
(5.23)
Определяется суммарный прогиб конца шпинделя и жесткость по формулам 5.24 и 55.25 соответственно:
![]() (5.24)
(5.24)
![]()
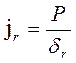 (5.25)
(5.25)
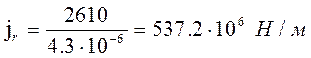 .
.
5. 2. 2. Осевая жесткость
Осевая жесткость практически полностью зависит от жесткости установленных в опорах подшипников. Поэтому данный расчет фактически сводится к определению жесткости подшипников, воспринимающих нагрузку в осевом направлении.
Осевую силу определим по формуле 5.26
Рх = (0,3…0,5)Рz = 1000 Н; (5.26)
Предварительный натяг определим по формуле 5.27
S = (1,5…2)Рх = 1500 Н; (5.27)
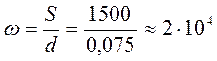 .
(5.28)
.
(5.28)
По величине w по графику [1] определяется осевая жесткость jо =2,5×108 Н/м и смещение в осевом направлении найдем по формуле 5.28:
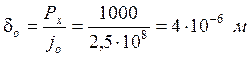 . (5.28)
. (5.28)
5.3. Анализ результатов
Величина допустимой погрешности [D], которая включает в себя помимо
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.