Проверочный расчет валов. Проверка подшипников качения. Расчет шлицевых соединений. Проверка прочности шпоночных соединений

5. 2. Проверочный расчет валов

Для упрощения расчетов, подвергнем проверочному расчету вал, находящийся перед шпинделем, как самый нагруженный. Проверим его на усталостную прочность и жесткость.

5.2.1. Выбор расчетной схемы и определение расчетных нагрузок

Проверке подвергается наихудший вариант нагружения вала, выявить который заранее не представляется возможным. Поэтому ведем расчет при всех случаях нагружения, при этом будет представлен расчет при зацеплении 1-1 (первое зацепление неподвижных колес и первое зацепление блока зубчатых шестерен), а остальные результаты сведены в табл.5.1.

Составим  схему сил, действующих на вал (рис. 5.1) и определим их значения.

Значения сил в зацеплении первой зубчатой передачи определим по формулам (5.2),(5.3) и (5.4).

Окружная сила в первом зацеплении 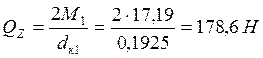   ;           (5.2)       

Радиальная сила в первом зацеплении                                                                                                                                                  (5.3)

Результирующая сила 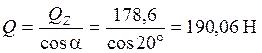;                                        (5.4)

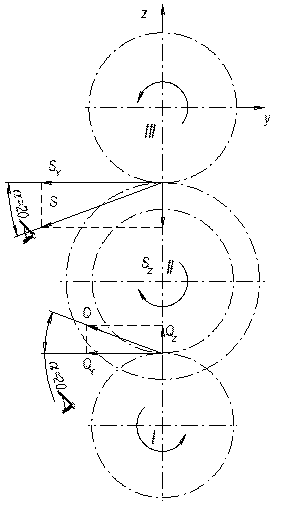
Рис. 5.1. Схема сил, действующих на вал

Окружная сила во втором зацеплении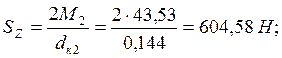   

Радиальная сила во втором зацеплении   

Результирующая сила .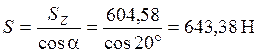                                                         

Построим расчетную схему вала. Для этого составим схемы нагружения вала в двух взаимно перпендикулярных плоскостях и наметим опасные сечения (рис. 5.2).

Рассмотрим силы и моменты, действующие в плоскости ZOY, и определим реакции в опорах:

SМ_А = Q_z×0,044 - S_z×(0,044+0,188) + B_z×0,375 = 0,

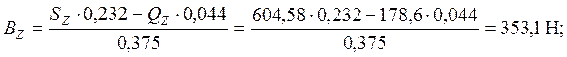
SМ_B = -Q_z×(0,375-0,044) + S_z×0,143 - A_z×0,375 = 0,

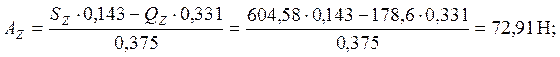
Проведем проверку:

SZ = Q_z - S_z + А_z + B_z = 178,6 – 604,58 + 72,91 + 353,07 = 0;

Изгибающий момент для наиболее опасного сечения:

М_zох = B_z×0,143 = 353,07×0,143 = 50,49 Н×м.

Рассмотрим силы и моменты, действующие в плоскости YOX, и определим реакции в опорах:

SМ_А = Q_Y×0,044 + S_Y×(0,044+0,188) – B_Y×0,375 = 0,

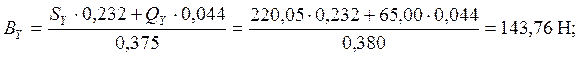
SМ_B = Q_Y×(0,375-0,044) + S_Y×0,143 – A_Y×0,375 = 0,

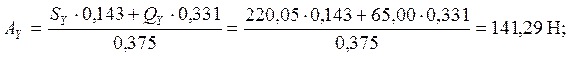
Проведем проверку:

SY = -Q_Y - S_Y + А_Y + B_Y = -65,00 – 220,05 + 143,76 + 141,29 = 0;

Изгибающий момент для наиболее опасного сечения:

М_yох = B_y×0,143 = 143,76×0,143 = 20,56 Н×м.

Суммарный изгибающий момент можно найти, как

                                                              ,                                           (5.5)

Суммарный момент, действующий на вал:

Таблица 5.1 Реакции опор и расчетные нагрузки

Результаты расчета показали, что схема зацепления 1-1 является наихудшим вариантом нагружения вала, поэтому дальнейшие расчеты проводим именно по этой схеме.

Конструктивная и расчетная схемы вала представлена на рис. 5.2. Построим эпюры изгибающих моментов, суммарного изгибающего момента и крутящего момента. Для этого намечаем опасные сечения I-I, II-II и III- III. Определим изгибающий момент в этих сечениях:

М_zохI = A_z×0,044 = 72,91×0,044 = 3,21 Н×м.

М_zохII = A_z×(0,044+0,153) + Q_z×0,153 = 72,91×(0,044+0,153) + 178,6×0,153 = 41,69 Н×м.

М_zохIII = B_z×0,143 = 353,07×0,143 = 50,49 Н×м.

М_yохI = A_y×0,044 = 141,29×0,044 = 6,22 Н×м.

М_yохII = A_y×(0,044+0,153) – Q_y×0,153 = 141,29×(0,044+0,153) + 65×0,153 = 17,89 Н×м.

М_yохIII = B_y×0,143 = 143,76×0,143 = 20,56 Н×м.

Суммарный изгибающий момент:

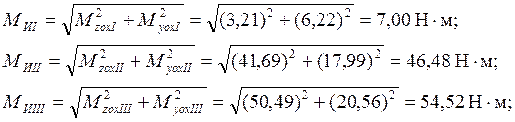
Суммарный момент, действующий на вал:

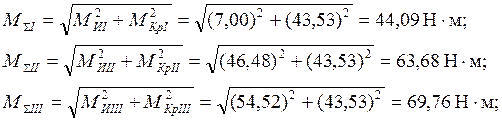
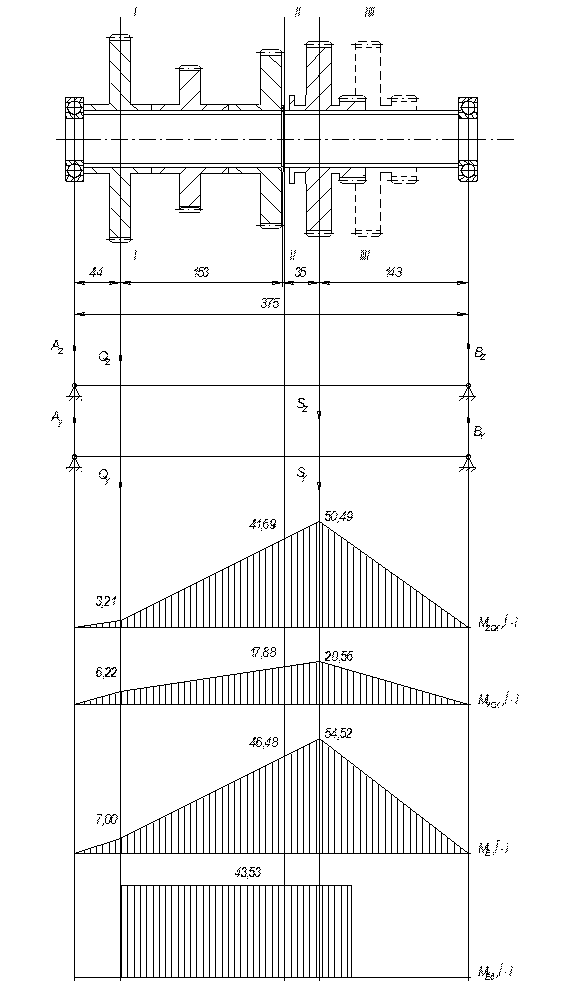
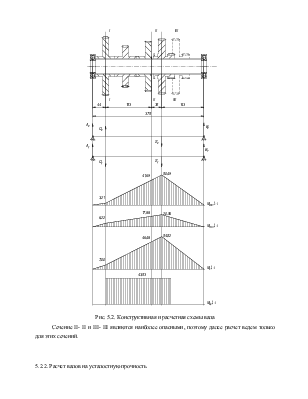
Рис. 5.2. Конструктивная и расчетная схемы вала

Сечение II- II и III- III являются наиболее опасными, поэтому далее расчет ведем только для этих сечений.

5.2.2. Расчет валов на усталостную прочность

Расчет на усталостную прочность сводится к определению коэффициентов запаса прочности в опасных сечениях и сравнению их с допускаемыми.

При совместном действии напряжений кручения и изгиба запас сопротивления усталости определяют по формуле 5.6.

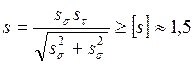                                                            ,                                         (5.6)

где 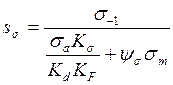 – запас сопротивления усталости только по изгибу,           (5.7)

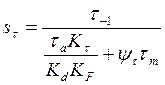        – запас сопротивления усталости только по кручению,      (5.8)

где s_а и t_а – амплитуды переменных составляющих циклов напряжений,

s_m = 0 и t_m = t_а – постоянные составляющие;

К_d = 0,58 и К_F = 0,8 – масштабный фактор и фактор шероховатости.

y_s и y_t  – коэффициенты, корректирующие влияние постоянной составляющей цикла напряжений на сопротивление усталости.

Определим запас сопротивления усталости в сечении II-II.

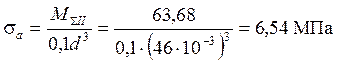,                                                                         (5.9)

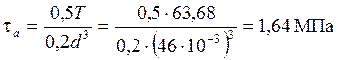;                                                                        (5.8)

y_s = 0,15 и y_t = 0,1 – коэффициенты, корректирующие влияние постоянной составляющей цикла напряжений на сопротивление усталости;

К_s = 1,9 и К_t = 1,4 – эффективные коэффициенты концентрации напряжений при изгибе и кручении;

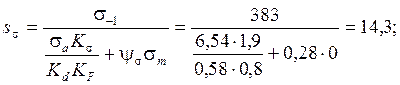
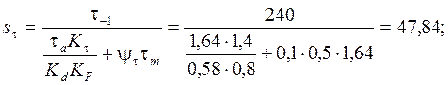
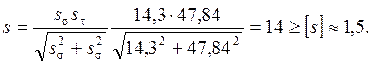
Определим запас сопротивления усталости в сечении III-III.

,                                                                                

;                                                                                  

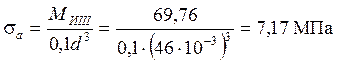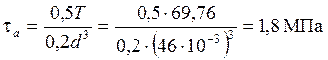y_s = 0,15 и y_t = 0,1 – коэффициенты, корректирующие влияние постоянной составляющей цикла напряжений на сопротивление усталости;

К_s = К_t =1 при расчете по внутреннему диаметру шлицов;

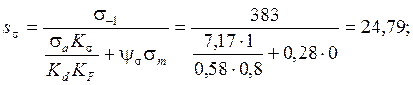
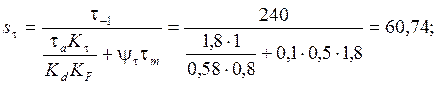
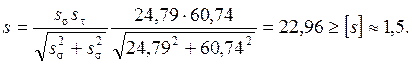
5.2.3. Расчет  на жесткость

При расчете на жесткость необходимо соблюдение неравенств [1]:

                                                                          y £ [y];                                                       (5.9)

                                                                          q £ [q],                                                     (5.10)

где y, [y] – прогибы сечения вала, расчетный и допускаемый, мм; q, [q] – угол поворота вала в подшипнике, расчетный и допускаемый, рад.

Допускаемые значения прогиба и угла поворота

[y] = (0,01…0,03)m, где m – модуль зацепления.

[q] = 0,005 рад.

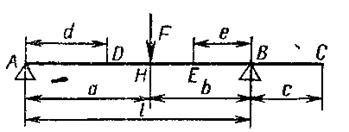
Рис. 5.3. Расчетная схема угла поворота и прогиба вала

Значения прогиба, угла поворота под шестерней и угла поворота вала в подшипнике можно определить из приближенных зависимостей:

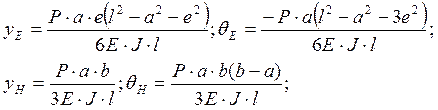                                                    (5.11)

где Е = 2,1×10⁵ Н/мм² – модуль упругости;

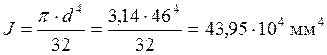 – полярный момент инерции сечения вала.

Определим значение прогиба в опасном сечении III по формуле 5.11.

 ;

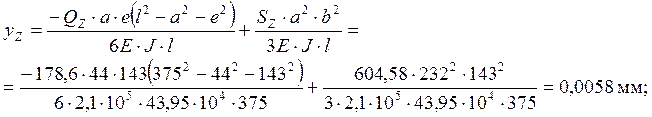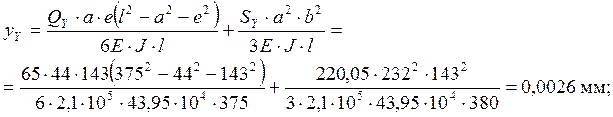
Сравниваем полученное значение с допустимым значением прогиба:

;

Значения угла поворота под шестерней:

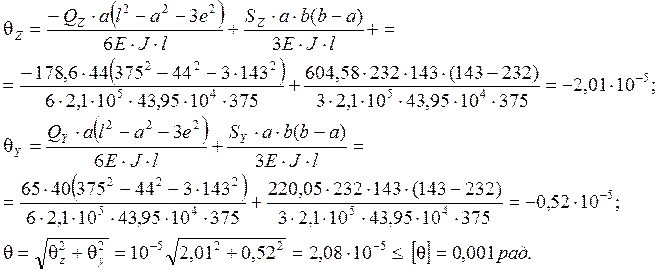
Значение угла поворота вала в опорах А и В занесем в табл