


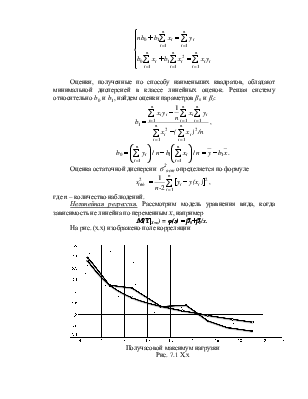


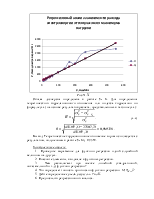

максимумом нагрузки Рmax (MВт)и расходе электроэнергии W (ГВТ∙ч); оценить точность подбора вида функции регрессии
Основные понятия регрессии
При изучении статистических зависимостей форму связей можно характеризовать функцией регрессии (линейной, квадратичной, показательной и т. д.)
Функция регрессии имеет значение при статистическом анализе зависимостей между переменными и может быть использована для прогнозирования одной из случайных переменных, если известно значение другой случайной переменной. Точность такого прогноза определяется дисперсией условного распределения.
Для оценки линейной функции регрессии необходимо знать аналитический вид двухмерного распределения (X,Y), а далее оценить параметры двухмерного распределения. На практике, для оценки чаще всего располагают выборкой ограниченного объема, по которой нужно найти вид функции регрессии. Для характеристики формы связи при изучении зависимости используют понятие кривой регрессии.
Кривой регрессии Y по X (или X по Y) называют условное среднее значение случайной переменной Y, рассматриваемое как функция определенного класса, параметры которой находят методом наименьших квадратов по наблюденным значениям двумерной случайной величины (x, y), т.е.
![]() или
или ![]()
Кривую регрессии называют также эмпирическим
уравнением регрессии или просто уравнением регрессии. Кривая регрессии,
выражаемая как ![]() , минимизирует среднюю квадратическую погрешность
прогноза Y по X.
, минимизирует среднюю квадратическую погрешность
прогноза Y по X.
Под регрессией понимается функция, предназначенная для описания зависимости изменения результативных признаков под влиянием колебаний признаков-факторов. Наличие корреляционной связи между параметрическими признаками позволяет приближенно предоставить значения результативного признака в виде некоторой функции от величины одного или нескольких факторных признаков.
Функцию, показывающую корреляционную зависимость между признаками, принято называть уравнением регрессии. Если оно связывает лишь два признака, то представляет собой уравнение парной регрессии; если отражает зависимость результативного признака от двух, трех и более факторных признаков – это уравнение множественной регрессии.
При выявлении корреляционной формы, связывающей результативный признак с одним факторным, помогает графическое изображение связи в виде поля корреляции. Обычно считают, что увеличение результативного и факторного признаков в арифметической прогрессии при прямой связи требует применения прямолинейной, а при обратной – гиперболической регрессии.
Составление уравнения регрессии означает прежде всего определение его параметров, используя для этого, где возможно, способ наименьших квадратов, согласно которому сумма квадратов отклонений фактических значений результативного признака от теоретических значений, рассчитанных по уравнению регрессии, должна быть наименьшей, т. е.
![]()
где ![]() –
фактические варианты признака-результата;
–
фактические варианты признака-результата; ![]() – теоретические
– теоретические
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.