Проектирование привода общего назначения с цилиндрическим редуктором

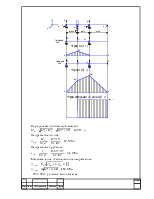
1. Разработка вариантов принципиальных кинематических схем привода. Выбор наиболее предпочтительной схемы привода.

1.1. Найдем скорость вращения тяговой звездочки конвейера:

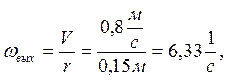
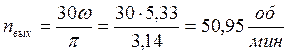    , где

ω_вых – угловая скорость вращения тяговой звёздочки,

V – скорость конвейера,

r – радиус тяговой звездочки,

n – частота вращения на тяговой звездочке конвейера.

1.2. Найдем необходимую мощность:

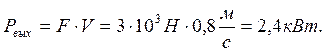, где

Р_вых – необходимая мощность двигателя,

F – окружное усилие на тяговой звездочке конвейера.

1.3. Зная синхронные скорости вращения двигателей (1000, 1500, 3000 об/мин) определим общее передаточное отношение привода:

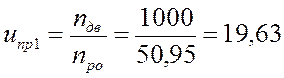
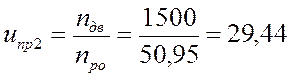
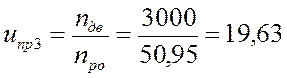   , где

общее передаточное отношение привода,

частота вращения двигателя,

частота вращения рабочего органа.

1.4. Разработаем варианты кинематических схем привода с двухступенчатым редуктором.

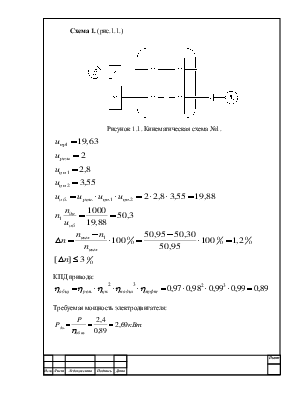
Схема 1. (рис.1.1.)

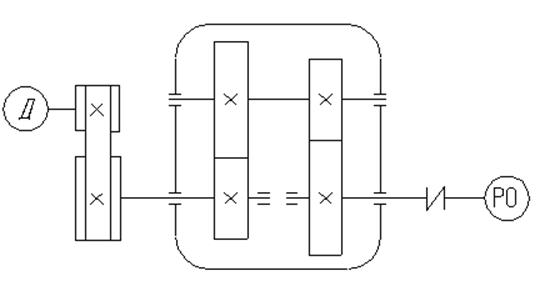
Рисунок 1.1. Кинематическая схема №1.

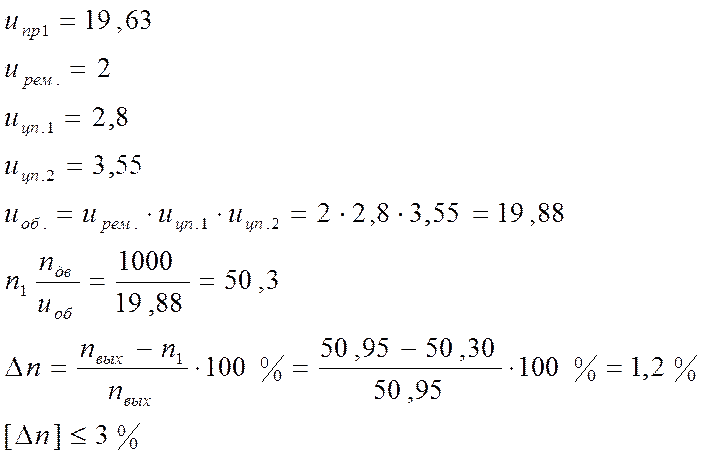
КПД привода:

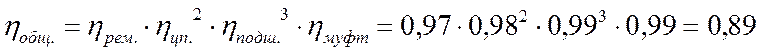
Требуемая мощность электродвигателя:

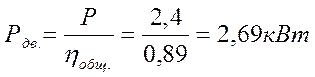
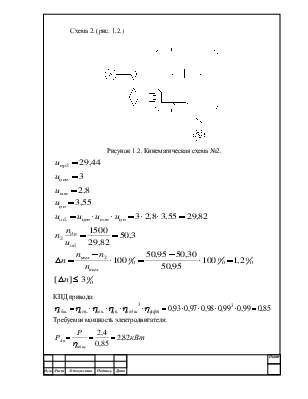
Схема 2.(рис. 1.2.)

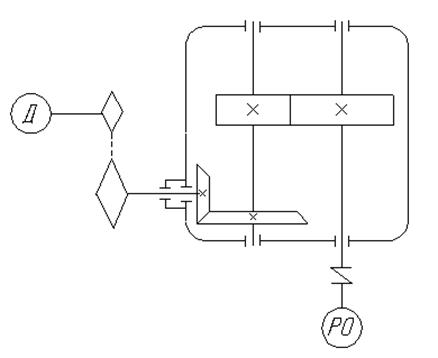
Рисунок 1.2. Кинематическая схема №2.

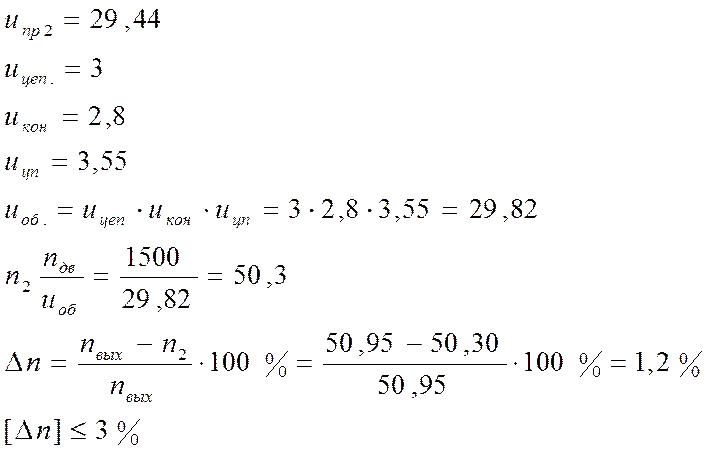
КПД привода:

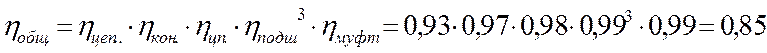
Требуемая мощность электродвигателя:

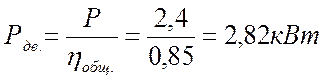
Схема 3.(рис. 1.3.)

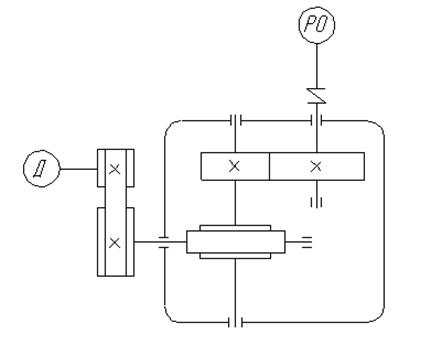
Рисунок 1.3. Кинематическая схема №3.

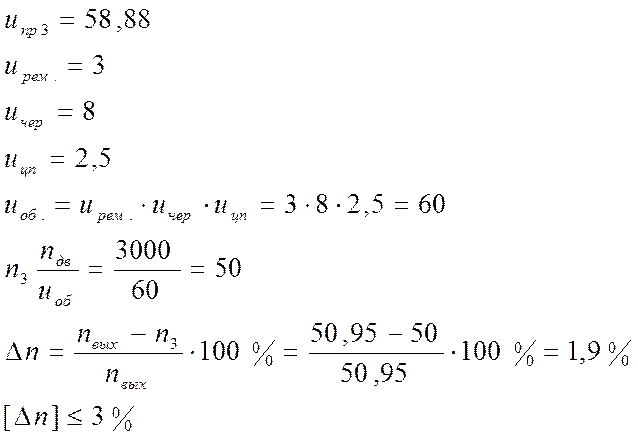
КПД привода:

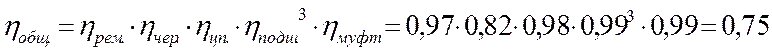
Требуемая мощность электродвигателя:

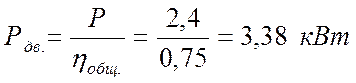
1.5. Выбор наиболее предпочтительной схемы привода.

Выбираем первую схему. 

В этой схеме используется электродвигатель со скоростью вращения

n = 1000 об/мин, который имеет относительно малые габаритные размеры.

КПД  данной схемы наибольший и составляет 89,5%.

Прямозубая цилиндрическая передача проста в изготовлении.  При ее использовании практически отсутствуют осевые силы, что позволяет применять простые подшипниковые узлы, также с легкостью выполняется условие смазки.

2. Кинематический расчет привода

2.1. Выбор двигателя.

Из таблицы выбираем ближайший по мощности электродвигатель с нормальным пусковым моментом. [1, стр. 390]

4А112МА6У3, имеющий

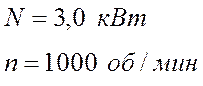
2.2. Определяем числа оборотов и крутящих моментов на валах.

Число оборотов первого вала:

Число оборотов второго вала: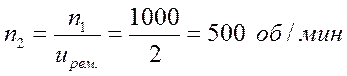 

Число оборотов третьего вала: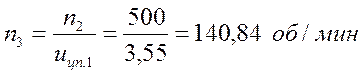

Число оборотов четвертого вала: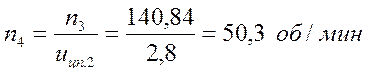

Момент на первом валу:

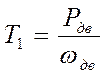
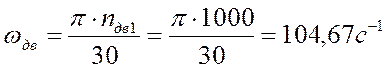
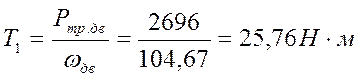
Момент на втором валу:

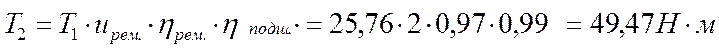
Момент на третьем валу:

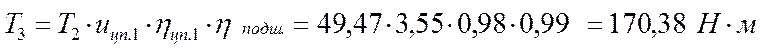
Момент на четвертом валу:

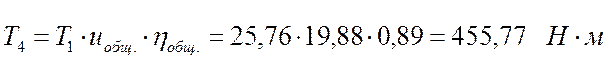
3. Расчет зубчатых колес редуктора.

 3.1. Выбор материала.

   Желая получить сравнительно небольшие габариты и невысокую стоимость редуктора, выбираем для изготовления зубчатых колес сравнительно недорогую сталь 40, при термообработке – нормализация, с твердостью для быстроходной ступени: для шестерни НВ^б_ш =140, для колеса НВ^б_к =130, а для тихоходной ступени: для шестерни НВ^т_ш =160, для колеса НВ^е_к =150. [3,стр.67]

3.2. Расчет допускаемых контактных напряжений.

а) Быстроходная ступень.

Допускаемое контактное напряжение:

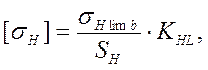  [2, стр.167-173]

где - базовый предел контактной выносливости активных поверхностей зубьев; - коэффициент безопасности; - коэффициент долговечности, по контактной выносливости.

Для  нормализации предел контактной выносливости ,

Коэффициент долговечности:

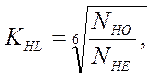
где N_HO – базовое число циклов;  ,  - эквивалентное число циклов.

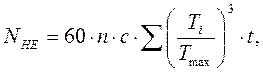
где - частота вращения вала, на котором насажена шестерня (колесо);  - число колес, одновременно сцепленных с шестерней;  - время работы шестерни.

 для шестерни;

 для колеса;

ч.

где  - срок службы в годах, - коэффициент годового использования,  - коэффициент суточного использования.

Для шестерни:

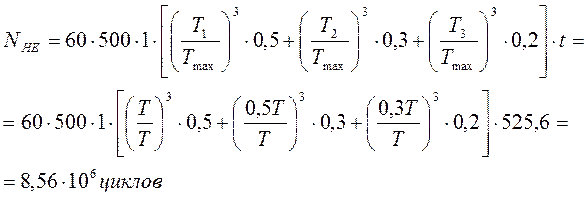
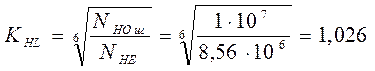
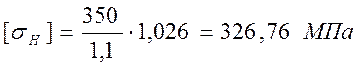
Для колеса:

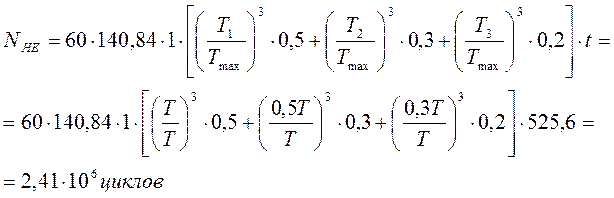
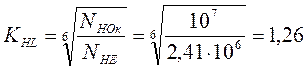
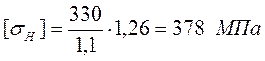
б) Тихоходная ступень.

Для  нормализации предел контактной выносливости,

.

Для шестерни с термообработкой - нормализация НВ_ш=160, для колеса с термообработкой - нормализация НВ_к=150.

для шестерни;

для колеса;

ч.

Для шестерни:

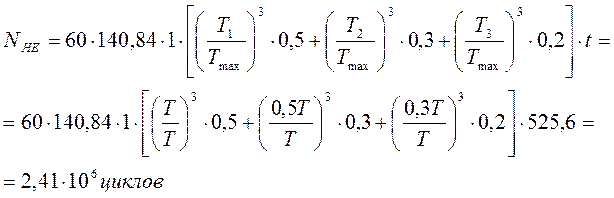
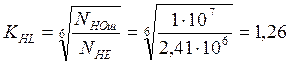
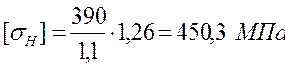
Для колеса:

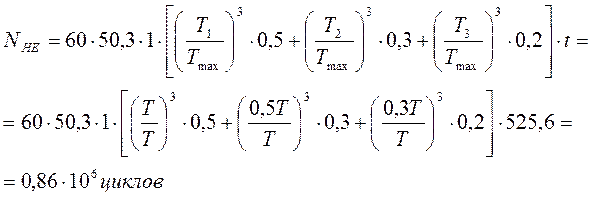
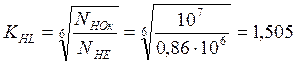
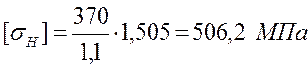
3.3. Расчет допускаемых напряжений на выносливость при изгибе.

а) Быстроходная ступень.

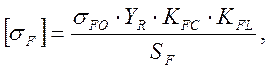   [2, стр. 173-174]

где  - коэффициент безопасности, - предел выносливости при изгибе,  - шероховатость поверхности,  - коэффициент, учитывающий характер приложения нагрузки,  - коэффициент долговечности.

Для колеса:

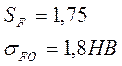
 для шестерни;

 для колеса;

(при нормализации)

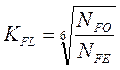, где - базовое число циклов,  - эквивалентное число циклов.

 для шестерни;

 для колеса.

Для шестерни:

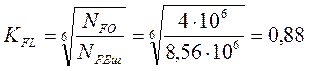
Так как результат меньше 1, то

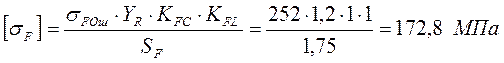
Для колеса:

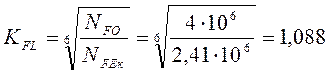
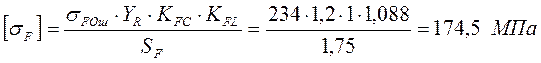
б) Тихоходная ступень.

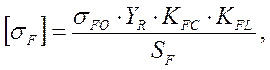
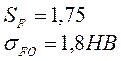
 для шестерни;

 для колеса;

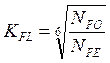, где - базовое число циклов,  - эквивалентное число циклов

 для шестерни;

 для колеса.

Для шестерни:

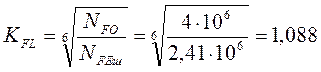
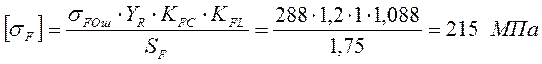
Для колеса:

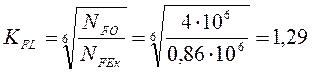
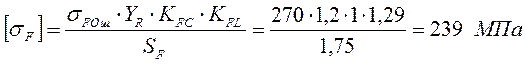
3.4. Расчет геометрических параметров передачи.

а) Тихоходная ступень.

   В соосном редукторе межосевые расстояния быстроходной и тихоходной ступеней равны  Начинают обычно расчет с тихоходной ступени как более нагруженной.  [1, стр.17]

Межосевое расстояние:

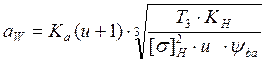, где

- передаточное отношение ступени;

К_a =450 (для прямозубых передач);

 - наименьшее допускаемое контактное напряжение ступени;

- момент на валу с шестерней;

- коэффициент, учитывающий неравномерность распределения нагрузки между зубьями;

 - коэффициент учитывающий неравномерность распределения нагрузки по ширине венца;

- динамический коэффициент;

 - коэффициент ширины венца.

;

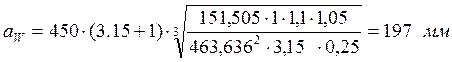по ГОСТ  2185-66 принимаем межосевое расстояние .

Модуль зубьев: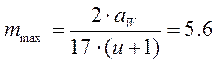        

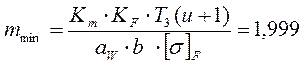
Принимаем

Суммарное число зубьев: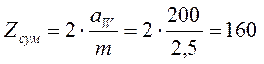

Число зубьев шестерни: 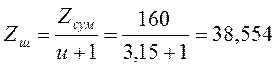, принимаем

Число зубьев колеса:

Действительное передаточное отношение: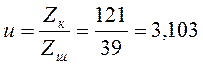

Ошибка по передаточному отношению:

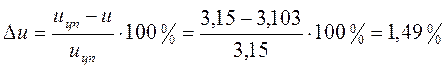
Делительные диаметры:

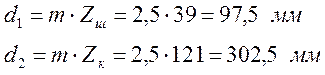
Диаметры вершин:

Диаметры впадин:

Ширина шестерни:

Проверка на контактную выносливость:

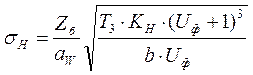
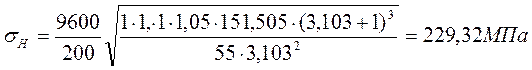
Проверка на изгиб:

Для колеса: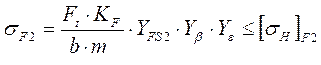 

Для шестерни: 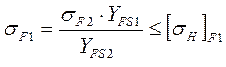   ,где

Y_FS = 3,59 – коэффициент учитывающий форму зуба;

– коэффициент учитывающий угол наклона зуба;

- коэффициент учитывающий степень точности;

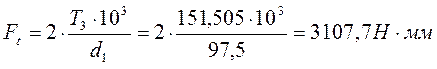
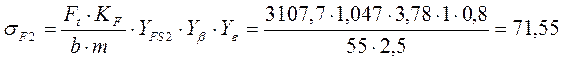
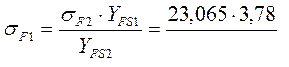
 - условие выполняется.

б) Быстроходная ступень.

Из условия соосности

 - коэффициент ширины венца.

Ширина венца колеса:

Модуль зубьев:

Принимаем

Суммарное число зубьев: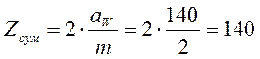

Число зубьев шестерни: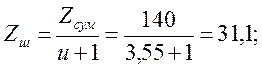

Принимаем

Число зубьев колеса:

Действительное передаточное отношение: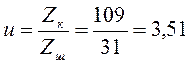

Ошибка по передаточному отношению:

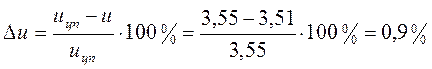
Делительные диаметры:

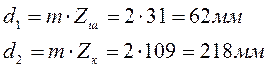
Диаметры вершин:

Диаметры впадин:

Ширина шестерни:

Проверка на контактную выносливость:

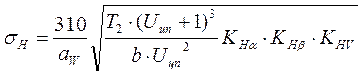
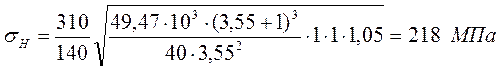
 - Условие выполняется.

Проверка на изгиб:

Для шестерни: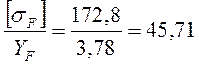

Для колеса: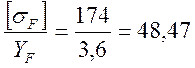 

Расчет ведем для шестерни.

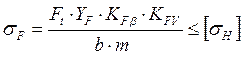, где

Y_F = 3,78 – коэффициент учитывающий форму зуба;

K_Fb = 1,05 – коэффициент неравномерности распределения нагрузки по длине контактной линии;

K_FV = 1,2 – коэффициент динамической нагрузки .

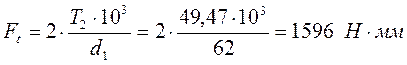
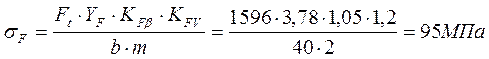
 - условие выполняется.

4. Предварительный расчет валов.

Быстроходный вал. (рис.4.1.)

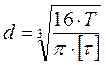   [1, стр.161] - расчетный диаметр выходного конца вала,

где  - допускаемое напряжение;

Т – момент на валу;

n = 1,75 - коэффициент запаса прочности;

k = 1,5 - коэффициент концентрации напряжения;

τ_-1= 0,43·σ_B  = 227,9 МПа – предел выносливости,

где σ_B=530 МПа –  предел прочности для стали 40.

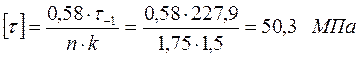, принимаем

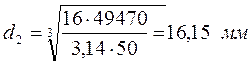
принимаем ; диаметр под подшипник ; диаметр под шестерню; диаметр буртика .

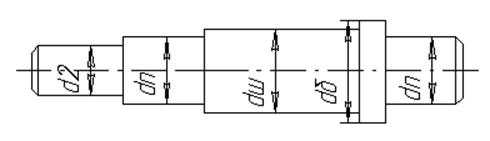
Рисунок 4.1. Быстроходный вал.

Промежуточный вал. (рис.4.2.)

,

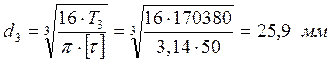принимаем ; диаметр под подшипник  ;

диаметр под колесо ,  диаметр буртика

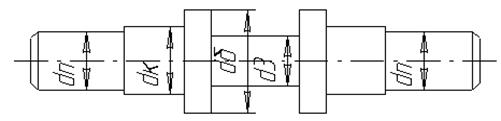
Рисунок 4.2. Промежуточный вал.

Тихоходный вал. (рис.4.3.)

,

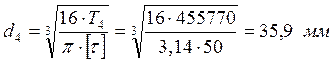 принимаем ; диаметр под подшипник ; диаметр под колесо ; диаметр буртика .

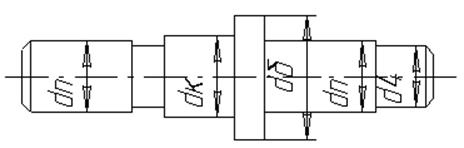
Рисунок 4.3. Тихоходный вал.

5. Конструктивные размеры шестерни и колеса.

Быстроходная ступень:

Шестерня:                                          Колесо:

Шестерню изготавливаем без ступицы.   [1, стр. 233]

Для колеса:

Диаметр ступицы ;

Длина ступицы , принимаем ;

Толщина обода , принимаем ;

Толщина диска ;

Диаметр отверстий ,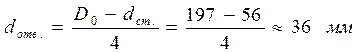

где Dо – внутренний диаметр обода;

Диаметр центровой окружности .

Тихоходная ступень:

Шестерня:                                Колесо:

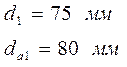
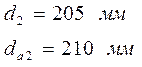
Шестерню изготавливаем без ступицы.

Для колеса:

Диаметр ступицы ;

Длина ступицы , принимаем ;

Толщина обода , принимаем ;

Толщина диска .

Диаметр отверстий ,

Диаметр центровой окружности .

7. Расчет валов на полную статическую прочность.

1) Быстроходный вал.   

Определяем силы в зацеплении:

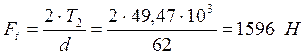
Определяем реакции в опорах:

YOZ: ; 

          ;

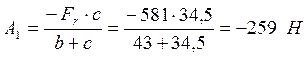
XOZ: ; , где 

         ;

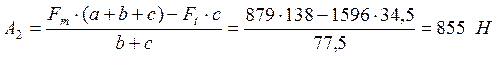
Строим эпюры моментов:

:            

     :

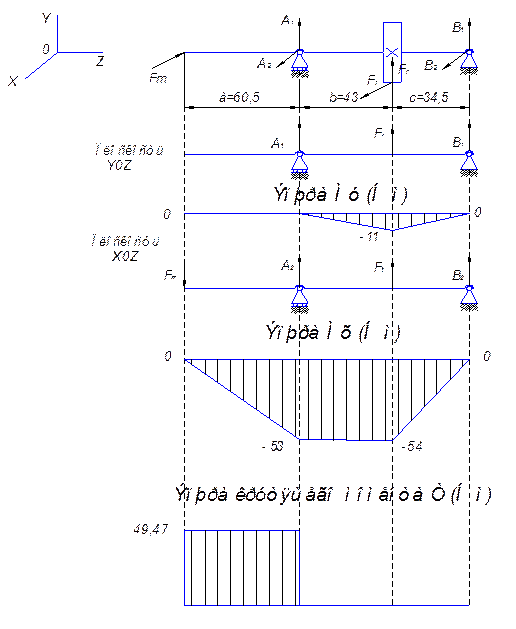
Определяем изгибающий момент:

Напряжение изгиба:

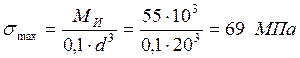
Напряжение кручения:

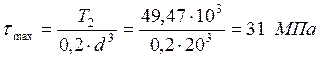
Максимальное эквивалентное напряжение:

, где      

-предел текучести материала;

-коэффициент запаса прочности по пределу текучести;

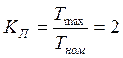-коэффициент перегрузки;

       - условие выполняется.

2)  Промежуточный вал.

Определяем силы в зацеплении:

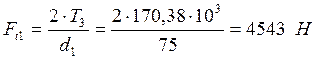
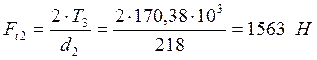
Определяем реакции в опорах:

YOZ: ; 

          ;

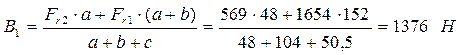
XOZ: ;

         ;

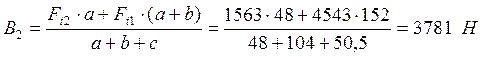
Строим эпюры моментов:

:            

     :

Определяем изгибающий момент:

Напряжение изгиба:

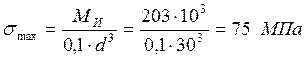
Напряжение кручения:

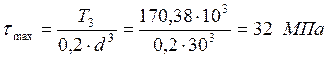
Максимальное эквивалентное напряжение:

,

  - условие выполняется.

   3) Тихоходный вал.    

Определяем силы в зацеплении:

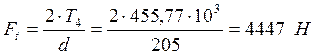
Определяем реакции в опорах:

YOZ: ; 

          ;

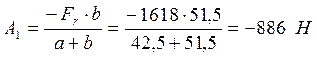
XOZ: ; , где

         ;

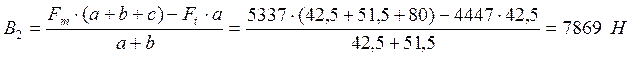
Строим эпюры моментов:

:            

     :

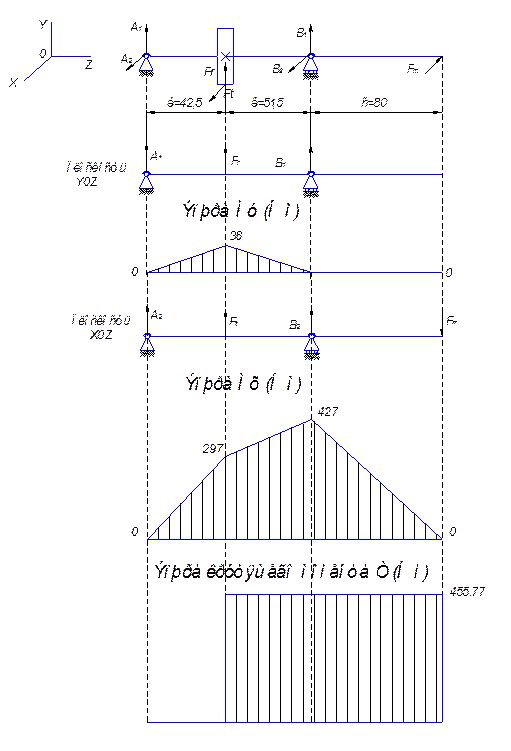
Определяем изгибающий момент:

Напряжение изгиба:

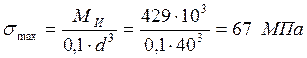
Напряжение кручения:

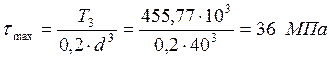
Максимальное эквивалентное напряжение:

,

   - условие выполняется.

8. Подбор и проверка подшипников.

1) Расчет подшипников быстроходного вала.

Рисунок 8.1. Расчетная схема подшипников быстроходного вала.

Принимаем шарикоподшипники радиальные однорядные средней серии 304, для которых грузоподъемность динамическая С = 15,9 кН, статическая С₀ = 7,8 кН.

Y_A = A₁ = -259 H;    X_A = A₂ = 855 H;

Y_B = B₁ = -322 H;   X_B = B₂ = -1572 H.

Суммарные реакции:

Выполняем проверочный расчет только для подшипника правой опоры, как наиболее нагруженной.

Определяем эквивалентную радиальную нагрузку по формуле:

Р_r = (XVF_r + YF_a)K_бK_т, где

            F_r, F_a – радиальная и осевая нагрузки;

X=1, Y=0 – коэффициенты радиальной и осевой нагрузок;

V=1 – коэффициент вращения, зависящий от того, какое кольцо подшипника вращается (при вращении внутреннего кольца V = 1, наружного V = 1,2);

К_б =1,5 – коэффициент безопасности, учитывающий характер нагрузки;

К_т =1 – температурный коэффициент.

 P_r = 1×1×1605×1,5×1 = 2407 Н.                

Определим расчетную долговечность подшипника (ч):

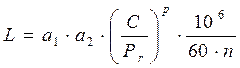
, где

n =500 – частота вращения кольца, об/мин;

p – показатель степени ( p = 3 – для шариковых);

а₁=1 –   коэффициент надежности;

а₂=0,75 –  обобщенный коэффициент совместного влияния качества металла и условий эксплуатации;

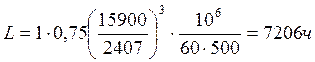
Найденная долговечность приемлема.

2) Расчет подшипников промежуточного вала.

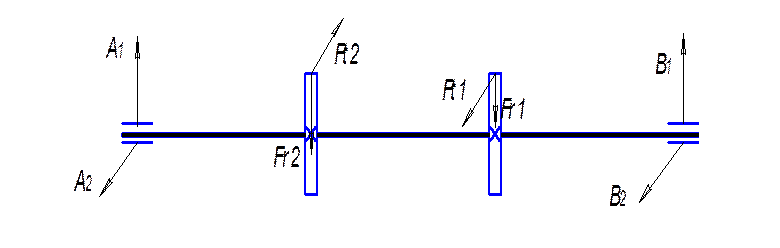
Рисунок 8.2. Расчетная схема подшипников промежуточного вала.

Принимаем шарикоподшипники радиальные однорядные средней серии 306, для которых грузоподъемность динамическая С = 28,1 кН, статическая С₀ = 14,6 кН.

Y_A = A₁ = 847 H;    X_A = A₂ = 2325 H;

Y_B = B₁ = 1376 H;   X_B = B₂ = 3781 H.

Суммарные реакции:

Выполняем проверочный расчет только для подшипника правой опоры