Вивчення особливостей роботи і використання скінченних автоматів (Лабораторна робота № DE-6), страница 2

Аналіз роботи автомата виконується з метою визначення стану в послідуючий тактовий момент часу  і передбачення послідуючих станів. Аналіз роботи автомата являється достатньо складною задачею, особливо при відсутності досвіду, тому рекомендується робити це поетапно, або крок за кроком. В такому плані рекомендуються слідуючі кроки:

·  Визначення станів на слідуючому тактовому моменті часу і значень виходів вхідної і вихідної комбінаційних функцій L_I , L_O;

·  Використання функцій L_I , L_O  для побудови таблиці станів, що повністю визначає слідуючий стан і значення виходу схеми для кожної комбінації поточного стану і входів;

·  Побудова діаграми тсанів, що містить в собі інформацію з попереднього кроку в графічній формі. 

В яості прикладу проведемо аналіз роботи схеми скінченого автомата з двома D- тригерами, що приведена на рис.

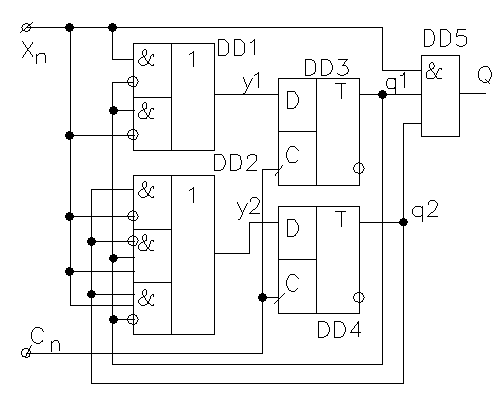Не знаючи деталей роботи схеми можемо визначити, що вхідна комбінаційна схема L_I представлена двома мікросхемами DD1 і DD2, входами яких являється вхідний сигнал X_n і сигнали, що визначають внутрішній стан автомата q1, q2. Виходами L₁  являються сигнали у1 і у2. В якості елементів внутрішньої пам’яті використовуються два динамічні D-  тригери DD3 і DD4. Вихідна комбінаційна схема L_O представлена трьохвходовим елементом 3І на мікросхемі DD5.

Тепер розглянемо поведінку схеми в роботі. При подачі синхросигналу С_n по його фрону кожен з тригерів відкриває свй D- вхід і передає його значення на вихід, що відповідає характеристичному рівнянню тригерів. Cигнали у1 і у2 являються встановлюючими (збуджуючими ( excitation)) для D- тригерів  в кожний тактовий момент часу. Логічні рівняння, що визначають встановочні сигнали, як функції поточного стану і вхідних сигналів називаються встановочними рівняннями (excitationequation)  і можуть біти отримані з схеми:

Використовуючи характеристичне рівняння D-тригерів, можемо записати слідуючі рівняння:

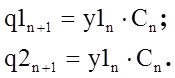                                                                       ( 3с )

підставляючи значення у1_n і у2_n  з встановочних рівнянь, отримаємо:

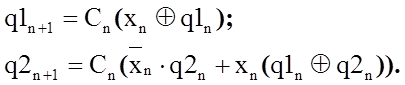                      ( 4с )

Отримані рівнянн(4с), які виражають значення стану автомата в n+1 момент часу в залежності від значень входів і поточного стану називаються перехідними рівняннями. Їх суть полягає в тому, що вони дають  можливість переджбачити  стан автомати в n+1  момент часу на основі інформації про стан і значення входів в n- й мометн часу.

Так як внутрішній стан автомата визначається значеннями виходів двох тригерів, то, відповідно, можна стверджувати, що існують лише 4 можливих стани автомата: (q1, q2) = 00,01,10,11. Для кожного стану в розглядяємому прикладі можливі лише два значення входу х: 0,1, так, що в загальному плані маємо лише 8 стан/ вхід комбінацій. ( В загальному плані автомат з s станами і k входами має  2 ^s+k стан/ вхід комбінацій).

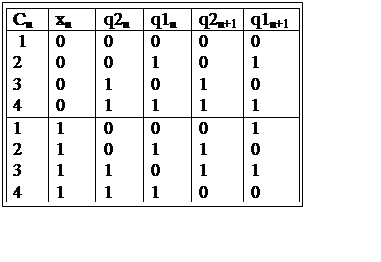Табл.4с.1 показує таблицю переходів скінченного автомата, яка побудована на основі аналізу рівнянь переходів для кожного з станів. З таблиці переходів витікає особливість роботи автомата, яка полягає в тому, що при х_n = 0  його внутрішні стани не змінюються, а при х_n = 1 він виконує функцію двійкового лічильника, тобто сигнал х_n являється таким, що забезпечує дозвіл ролботи схеми, як двійкового лічильника з максимальним значенням 11 =3.

В практиці проектування скінчених автоматів кожному з внутрішніх станів приписують конкретну назву, або конкретне позначення. Зробимо для розглядаємого автомата ,наприклад, такі позначення: q₀=00; q₁=01;q₂=10; q₃=11. Тоді таблиця станів дещо зміниться і прийме слідуючий вигляд: ( див. Табл.4.с2) 

                                  Табл.4.с2

Вихідний сигнал автмата визначається внутрішнім його станом і значенням вхідного сигналу і в відповідності до функції L_O   маємо

              ,

а автомат характеризується як автомат Мілі.