Вивчення особливостей роботи і використання тригерних схем (Лабораторна робота № DE-5)

можуть виводитись як незалежні і забезпечувати безпосереднє керування ЕП. Логічні рівні сигналів на входах R і S  залежать від значень вхідних логічних змінних х₁...х_n, сигналів синхронізації c₁...c_n, станів виходів елемента пам’яті Qта , та логіки роботи схеми керування. В залежності від призначення   тригерної схеми змінюється логічна функція схеми керування, кількість входів x_n, кількість та характер входів синхронізації. В зарубіжній інженерній практиці всі тригерні схеми розділяються на дві групи Перша з них –flip-flop-  характеризується тим, що вибірка вхідних сигналів і відповідна зміна виходів визначається в моменти дії тактових часових сигналів. (синхронні тригери).  Особливість другої група схем –latch- полягає в тому, що вони змінюють свій стан при появі вхідних сигналів і незалежно від наявності чи відсутності часових тактових сигналів. 

Розглянемо тригерні схеми на конкретних прикладах.

4.1.RS- тригери.

Схема RS- тригера, виготовлена на елементах 2АБО-НІ, приведена на рис.4.3а. Вона відповідає рис.4.1 тільки з різницею в позначеннях входів та виходів. Завдяки симметричному вигляду, вона часто називається симетричним RS-тригером. На рисунку 4.3,б приведено його умовне позначення. Стан тригера часто ототожнюється з сигналом на прямому Q виході – тобто тригер знаходиться в одиничному стані при Q=1, Q =0, та в нульовому – при Q=0, , =1.

Особливість схеми на відміну від комбінаційної схемотехніки полягає в тому, що будь-який із станів є стійким при відсутності вхідних сигналів. Дійсно, припустимо, що R=S=0, а =1. В цьому випадку на виході елемента DD1, буде зберігатись значення Q=0, що витікає з логіки роботи цього елемента, Значення Q=0 забезпечує значення виходу =1 елемента DD2, тобто забезпечується нульовий стан тригера.

Припустимо, що в цьому стані подано на вході комбінацію потенційних сигналів R=0, S=1. Тоді вихід елемента DD2 прийме значення =0, а відповідно до цього вихід елемента DD1 прийме значення Q=1. Тобто цією комбінацією вхідних  сигналів ми запишемо сигнал S=1 в тригер, як один біт інформації. Змінити стан тригера в попередній можливо протилежною комбінацією вхідних сигналів, тобто R=1, S=0. Якщо ми повторимо подачу цієї комбінації вхідних сигналів при Q=0,  а  =1, то стан тригера не зміниться. Таким чином стан виходів тригера в момент часу, слідуючий за моментом зняття вхідних сигналів залежить не тільки від комбінації вхідних сиг-налів, але й від попереднього стану його виходів. Тому для аналізу схеми необхідно розділення станів входів та виходів тригера в часі. Для цього попередні стани позначаються індексом n – S_n, R_n, Q_n. Стан тригера, який одержується в результаті комбінації вхідних сигналів  та значень виходів в  n-й момент часу позначається як Q_n+1 , _n+1.

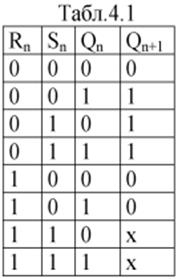
Завдяки такому розподіленню станів та вхідних сигналів в часі з’являється можливість використовувати логічні функції для запису алгоритму роботи тригерів. Повна таблиця станів RS-тригера (табл.4.1) описує функціювання цієї схеми. Особливість табл. 4.1 полягає в тому, що при S_n=R_n=1 незалежно від Q_n стан входів тригера  є невизначеним. Дійсно, якщо подати на обидва входи таку комбінацію сигналів, то на обох виходах з’являться логічні нулі. (Q_n+1=_n+1=0). Але якщо ці сигнали одночасно зняти, задавши Q_n+1=R_n+1=0, то стан виходів буде невизначеним. Це пов’язано з тим, що після зняття сигналів в кожному з логічних елементів буде протікати перехідний процес зміни станів і результат його буде залежати від швидкодії кожного з елементів. Остання є величиною невизначеною. Тому остання комбінація вхідних сигналів називаеться невизначеною, а перехід від цієї комбінації до нульової називається забороненим переходом