Афінним називається таке відображення площини (простору) на іншу площину (простір), при якому кожна пряма відображається в пряму (рис. 3.1). Афінне перетворення – це афінне відображення площини на себе.


Рис. 3.1. Приклад афінного перетворення
Математичний апарат афінних перетворень лежить в основі побудови векторних зображень в комп’ютерній графіці.
 1
1
Рис. 3.2.
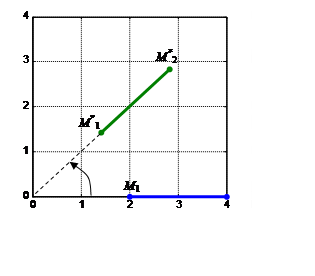
Нехай на площині визначено прямолінійну систему координат. Тоді будь-якій точці М ставиться у відповідність упорядкована пара чисел (x,y) - координати точки М. Перетворення, яке переводить точку М (x,y) в іншу точку М*(x*,y*) (рис. 3.2) задається формулами:
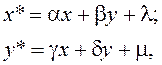 (3.1)
(3.1)
де a, b, l, g, d, m – довільні числа, зв’язані нерівністю:
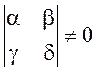
Серед множини можливих афінних перетворень площини особливу роль відіграють кілька важливих окремих випадків, що мають чітку геометричну інтерпретацію, а саме поворот, стиснення-розтягнення, відбиття та зсув. В табл. 3.1 наведено
|
№ |
Назва перетворення |
Геометрична інтерпретація |
Аналітична залежність |
||
|
1. |
Поворот навколо початку координат на кут j |
|
|
||
|
2. |
Стиснення вздовж координатної осі |
|
|
||
|
3. |
Відбиття відносно координатної осі |
|
|
||
|
4. |
Зсув |
|
|
Для ефективного представлення основних перетворень на базі матричних операцій застосовуються однорідні координати. В загальному вигляді матричний запис афінних перевторень:
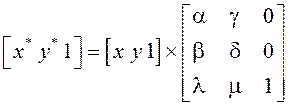 .
.
В тривимірному просторі матриця узагальненого афінного перетворення має вигляд:
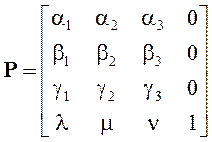 .
.
В бібліотеці Open GL перетворення фігур досягається шляхгм відповідного перетворення системи координат перед виводом фігури. Для перенесення системи координат застосовуються наступні процедури:
glTranslated(dx, dy, dz: double);
де dx, dy, dz – величини зсуву системи координат по відповідним осям.
glRotated(Angle, x, y, z: double);
де x, y, z – координати радіус-вектора, навоколо якого здійснюється поворот системи координат (довжина вектора має дорівнювати 1); Angle – кут повороту в градусах (додатній напрямок проти годинникової стрілки, від’ємний – за годинниковою стрілкою).
glScaled(kx, ky, kz: double);
де kx, ky,kz – коефіцієнти стиснення / розтягу масштабу відповідних координатних осей.
Для збереження поточного стану координатної системи застосовується процедура pushmatrix, а для його відновлення – popmatrix.
1. Вивести на екран зображення стрілки та перевірте роботу наведених вище процедур Open GL.
2. З застосуванням Open GL написати процедуру для виводу на екран зображення кола з центром в початку координат та радіусом 1.
3. Шляхом перетворення координат та виклику написаної процедури вивести на екран кілька кіл в різних позиціях та різного радіусу.
4. Переробити програму малювання графіка з попередньої лабораторної роботи, так, щоб по заданому інтервалу зміни координати х автоматично визначалися необхідні межі виводу по координаті y та на форму виводився весь графік функції цілком.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.