Математика \ Численные методы

Приближенное вычисление определенных интегралов. Методы прямоугольников и метод Симпсона, страница 2

     case  'RightRectangles'

        for i=1:n-1

            Sum = Sum + h*myfunc(func,a + i*h);

        end;

        Sum = h*myfunc(func,b) + Sum;

     case 'MediumRectangles'

        for i=1:n

            Sum = Sum + h*myfunc(func,((a + (i-1)*h)+(a + i*h))/2);

        end;

     otherwise

       error('This is impossible value')

 end

 res = Sum;

return

function res=myfunc(func,a);

f=func;

syms x

res=double(subs(f, x, a));

% myfunc = f(x)

function rez = R(func,str,a, b, n, j)

Er=abs(Integral(func,str,a,b,n)-Integral(func,str,a,b,n/2))/(2^j-1);

rez =Er;

function res=Error(func,str,a,b,n)

h=(b-a)/n;

x(1) = a;

for i=1:n+1

x(i+1)=x(i)+h;

end

switch str

    case 'Simpson'

        MK = Integral_diff(x, 4, n, func);

        res = abs((b-a)*h^4/180)*max(sqrt(sum(MK .* MK)));

    case 'Trapezium'

        MK=Integral_diff(x, 2, n, func);

        res = abs((b-a)*h^2/12)*max(sqrt(sum(MK .* MK)));

    case 'LeftRectangles'

        MK=Integral_diff(x, 1, n, func);

        res = abs((b-a)*h)*max(sqrt(sum(MK .* MK)));

    case 'MediumRectangles'

        MK=Integral_diff(x, 2, n, func);

        res = abs((b-a)*h^2/6)*max(sqrt(sum(MK .* MK)));

    case 'RightRectangles'

        MK=Integral_diff(x, 1, n, func);

        res = abs((b-a)*h)*max(sqrt(sum(MK .* MK))); 

end; 

function rez = Integral_diff(a, k, n, func)

dy = func;

syms x

for i=1:k

    dy = diff(dy);

end;

for i=0:n

    MK(i+1)=double(subs(dy, x, a(i+1)));

end;

rez = MK;

function res = script

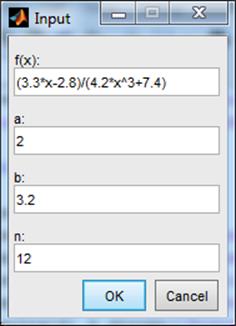
prompt = {'f(x):','a:','b:', 'n:'};

dlg_title = 'Input';

num_lines = 1;

def = {'(3.3*x-2.8)/(4.2*x^3+7.4)','2','3.2', '12'};

answer = inputdlg(prompt,dlg_title,num_lines,def);

func = answer{1};

a = str2num(answer{2});

b = str2num(answer{3});

n = str2num(answer{4});

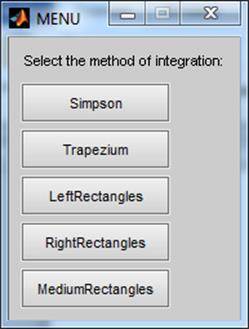
choice=menu('Select the method of integration:',  ...

'Simpson', 'Trapezium', 'LeftRectangles', 'RightRectangles', 'MediumRectangles');

 switch choice

        case 1

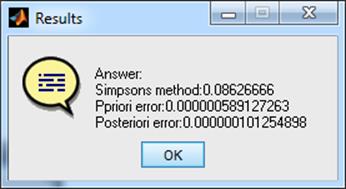
    results{1} = 'Answer:';

    results{2} = strcat('Simpsons method: ',...

    num2str(Integral(func,'Simpson',a,b,n),'%.8f'));

    results{3} = strcat('Ppriori error: ',...

    num2str(Error(func,'Simpson',a,b,n),'%.15f'));

    results{4} = strcat('Posteriori error: ',...

    num2str(R(func,'Simpson',a,b,n,4),'%.15f'));

        case 2

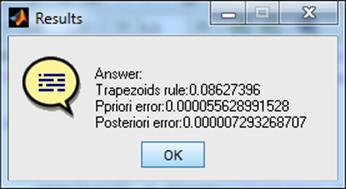
    results{1} = 'Answer:';

    results{2} = strcat('Trapezoids rule: ',...

    num2str(Integral(func,'Trapezium',a,b,n),'%.8f'));

    results{3} = strcat('Ppriori error: ',...

    num2str(Error(func,'Trapezium',a,b,n),'%.15f'));

    results{4} = strcat('Posteriori error: ',...

    num2str(R(func,'Trapezium',a,b,n,2),'%.15f'));

        case 3

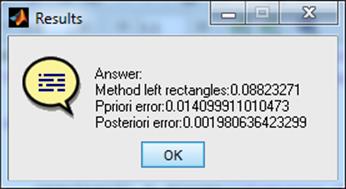
    results{1} = 'Answer:';

    results{2} = strcat('Method left rectangles: ',...

    num2str(Integral(func,'LeftRectangles',a,b,n),'%.8f'));

    results{3} = strcat('Ppriori error: ',...

    num2str(Error(func,'LeftRectangles',a,b,n),'%.15f'));

    results{4} = strcat('Posteriori error: ',...

    num2str(R(func,'LeftRectangles',a,b,n,1),'%.15f'));

        case 4

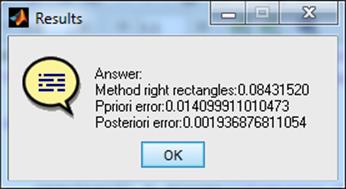
    results{1} = 'Answer:';

    results{2} = strcat('Method right rectangles: ',...

    num2str(Integral(func,'RightRectangles',a,b,n),'%.8f'));

    results{3} = strcat('Ppriori error: ',...

    num2str(Error(func,'RightRectangles',a,b,n),'%.15f'));

    results{4} = strcat('Posteriori error: ',...

    num2str(R(func,'RightRectangles',a,b,n,1),'%.15f'));

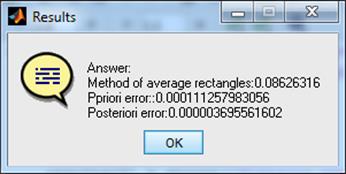
        case 5

    results{1} = 'Answer:';

    results{2} = strcat('Method of average rectangles: ',...

    num2str(Integral(func,'MediumRectangles',a,b,n),'%.8f'));

    results{3} = strcat('Ppriori error:: ',...

    num2str(Error(func,'MediumRectangles',a,b,n),'%.15f'));

    results{4} = strcat('Posteriori error: ',...

    num2str(R(func,'MediumRectangles',a,b,n,2),'%.15f'));

 end

helpdlg(results, 'Results');

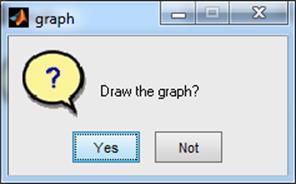
dlg=questdlg('Draw the graph? ','graph','Yes','Not','Yes');

switch dlg

case 'Yes'

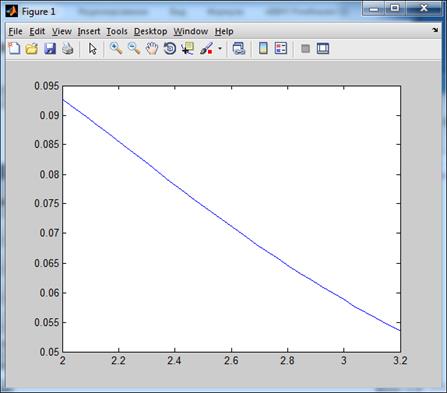
fplot(func,[a,b]);

case 'Not'

end;

end

                          

     

                 

                                         

                                               

Test

1.  Unit interval for Simpson's formula:

a)  h;

b)  2h;!!!

c)  3h;

2.  There are four points. Written the Simpson formula.

a)   ;

b)   ;

c)   formula can not be written;!!!

3.  Which method has a posteriori error of order two?

a)  the trapezoidal rule;!!!

b)  the method right rectangles; 

c)  the method of average rectangles;!!!

4.   Which we can find the error after calculating:

a)  posteriori;!!!

b)  priori;

c)  there is no such error;

5.  Geometric interpretation of the trapezoidal rule:

a)  integrand will replace a portion of [xi, xi + h] first-degree polynomial;!!!

b)  integrand will replace a portion of [xi, xi + h] zero - degree polynomial;

c)  integrand will replace a portion of [xi, xi + h] second - degree polynomial;

6.  Quadrature formula for n=1 (n-degree of the polynomial):

a)   ;!!!

b)   ;

c)   ;

7.  What method found approximation?

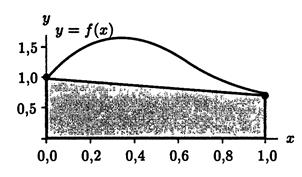
a)  the method right rectangles; 

b)  the trapezoidal rule;!!!

c)  the Simpson's method;

8.  The trapezoidal rule for integral. Given point: 1; 1.5; 2; 2.5; 3

a) 

b)   

c) 

9.  Runge formula for h and 3h for the Simpson's method

a) 

b) 

c) 

10. Which method described?

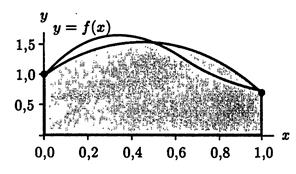
a)  the method right rectangles; 

b)  the Simpson's method;

c)  the method right rectangles; 

Скачать файл