







.
3.
Найти вероятность того, что
случайная величина примет значение в интервале (-1,1) и функцию распределения,
если известна плотность 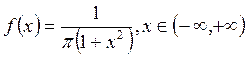 .
.
4. Из колоды в 36 карт две карты потерялись. Из оставшейся колоды наугад взяли две карты. Определить вероятность того, что среди них хотя бы одна карта бубновой масти.
1.
Найти математическое ожидание,
дисперсию и функцию распределения случайной величины с плотностью 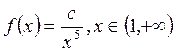 .
.
2. В условиях возникновения перегрева прибор выходит из строя с вероятностью 0.2, при повышенной вибрации – с вероятностью 0.4, а при одновременном возникновении перегрева и повышенной вибрации – с вероятностью 0.7. Прибор испытывают в условиях, когда с вероятностью 0.3 возникает повышенная вибрация, а с вероятностью 0.4 независимо от нее возникает перегрев. Найти вероятность выхода прибора из строя.
3.
Закон розподілу двомірної
випадкової величини ![]() задано таблицею:
задано таблицею:
|
-1 |
0 |
1 |
|
|
-1 |
3/32 |
5/32 |
1/32 |
|
0 |
5/32 |
8/32 |
3/32 |
|
1 |
3/32 |
3/32 |
1/32 |
Перевірити, що величини ![]() залежні, але
залежні, але ![]() та
та![]() незалежні.
незалежні.
1. .
2.
Найти функцию распределения,
математическое ожидание и вероятность того, что случайная величина примет
значение, по абсолютной величине не превосходящее ![]() , если
ее плотность равна
, если
ее плотность равна 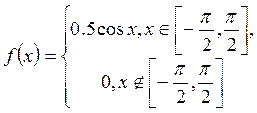 .
.
3. Охотник сделал три выстрела в дикого кабана, вероятность успеха равна 0.4. Если в кабана попадут две или три пули, кабан будет убит наверняка, при попадании одной пули – с вероятностью 0.6. Найти вероятность гибели кабана.
4.
Найти закон распределения
случайной величины ![]() , если
, если ![]() и
и
![]() - н.о.р. равномерные на отрезке
- н.о.р. равномерные на отрезке ![]() .
.
1. Два стрелка производят по 5 выстрелов, причем каждый стреляет по своим мишеням. Определить вероятность того, что у них будет по одинаковому числу попаданий, если вероятность успеха у них одинакова и равна 0.5.
2.
Найти математическое ожидание и дисперсию
случайной величины ![]() , если средние значения величин
равны 4 и (-3), дисперсии 9 и 4, а ковариация равна 2.
, если средние значения величин
равны 4 и (-3), дисперсии 9 и 4, а ковариация равна 2.
3. Определить вероятность того, что на 2000 клиентов страховой фирмы произойдет не менее 2 страховых случаев, если вероятность возникновения страхового случая равна 0.002.
1.
Плотность вероятности двумерной
случайной величины равна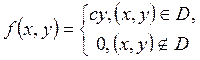 в области,
представляющей собой треугольник с вершинами (0,0),(2,0),(0,1). Определить
маргинальные распределения. Найти коэффициент корреляции.
в области,
представляющей собой треугольник с вершинами (0,0),(2,0),(0,1). Определить
маргинальные распределения. Найти коэффициент корреляции.
2. Из колоды в 36 карт наугад извлекают 6 карт. Найти вероятность того, что среди них хотя бы одна карта пиковой масти.
3. Брошены две игральные кости. Составить таблицу распределения суммы выпавших очков.
1. Из 20 студентов группы с равной вероятностью на лекции могут отсутствовать 0,1,2,3,4 или 5 . Преподаватель назвал наугад 5 фамилий, и все названные студенты присутствовали. Определить вероятность того, что в группе не было ни одного отсутствующего.
2.
Найти плотность и математическое
ожидание случайной величины, если 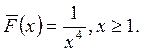
1. Производится 5 выстрелов по мишени, причем вероятность попадания при каждом выстреле равна 0.4. Составить закон распределения числа успешных выстрелов.
2. Случайная величина имеет распределение Пуассона с дисперсией 2. Что более вероятно: что значение этой величины окажется меньше 2 или больше 2?
3.
1.
Найти закон распределения
случайной величины ![]() , если
, если ![]() имеет
показательное распределение с параметром 1.
имеет
показательное распределение с параметром 1.
2. Случайная величина имеет нормальное распределение с математическим ожиданием 3 и дисперсией 1. Найти вероятности событий
![]() ,
, ![]() .
.
5. В урне 5 белых и 3 черных шара. Игрок А вытаскивает наугад 2 шара. После этого игрок В также вытаскивает два шара. Если они того же цвета, что у первого игрока, то А платит В три гривны, в противном случае игрок В выплачивает А две гривны. Найти среднее значение выигрыша каждого игрока.
1.
Найти закон распределения ![]() для независимых одинаково распределенных
равномерных величин на отрезке
для независимых одинаково распределенных
равномерных величин на отрезке ![]()
2.
Найти закон распределения
случайной величины ![]() , если
, если ![]() имеет
равномерное распределение на отрезке
имеет
равномерное распределение на отрезке ![]() .
.
3. Работают независимо друг от друга три элемента, время безотказной работы каждого из которых имеет показательное распределение со средним 1000 часов. Найти вероятность того, что за 1000 часов ни один из них не откажет.
1. Случайная величина имеет равномерное распределение со средним значением 2 и дисперсией 3. Найти функцию распределения.
2. Два стрелка стреляют по мишени. Первый попадает в цель с вероятностью 0.1, второй-0.7. Перед выстрелом они бросают монету для определения очередности. После выстрела оказалось, что мишень поражена. Найти вероятность того, что стрелял первый игрок.
1. Вероятность крупного выигрыша в некоторой лотерее равна 0.0015. Найти вероятность того, что на 2000 участников хотя бы один получит крупный
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.