Вращательное движение твердого тела

Министерство образования Российской Федерации

Санкт-Петербургский государственный горный институт

Имени Г.В. Плеханова

( технический университет)

Кафедра высшей математики

Расчетно-графическая работа

Вращательное движение твердого тела

Выполнил:  студент группы   ИЗ-03-1   _______________ Перчик А.В.

                                                                                 _{(подпись)}    

  

ОЦЕНКА:___________________

Дата:_______________________

Проверил:     доцент___ ________        Смирнова Н.Н.

                                                           (подпись)     

Санкт-Петербург

2004

1.  Условие задачи

Диск массой 560 г  вращается без начальной скорости вокруг своей оси. На него действуют пара сил с моментом 21,5 Дж и моментом сопротивления (κ•ω²) Дж, k=2,42 кг м². Сколько оборотов сделает цилиндр до того, как его угловая скорость станет равной 3,21 рад/с, если радиус диска равен 0,75 м.

2. Краткое теоретическое содержание

2.1. Определение основных величин, процессов, явлений, объектов, использованных при выполнении данного расчетно-графического задания:

Ось вращения тела – прямая, на которой лежат центры окружностей, по которым движутся точки твердого тела при его вращении. Окружности, по которым движутся точки тела, лежат в плоскостях, перпендикулярных к этой оси.

Угловая скорость - векторная величина, 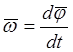, характеризующая быстроту вращения, ориентацию оси вращения в пространстве и направление вращения.

Угловое ускорение – векторная величина, 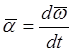, характеризующая изменение угловой скорости со временем.

Момент инерции тела – аддитивная  величина, равная сумме  произведений элементарных масс на квадрат их расстояния от некоторой оси. Единица измерения момента инерции [кг•м²]. Момент инерции характеризует распределение массы по объему и является мерой инертности тела при поступательном движении. Он не зависит от того, вращается ли тело, или находится в состоянии покоя и существует без относительного вращения, но зависит от распределения массы по этому телу. Поэтому  для различных геометрических тел различают и моменты инерции.

Пара сил – две равные по модулю и противоположно направленные силы, не действующие вдоль одной прямой.

Момент силы – векторная величина, , модуль которой равен произведению силы на плечо: . Если на тело действует 2 момента сил, вызывающих вращение в противоположном направлении, то один из них условно считают положительным, а второй отрицательным.

Плечо – кратчайшее расcтояние от оси вращения до линии действия силы.

2.2 Законы, соотношения, использованные при решении. Пояснение ко всем величинам, входящим в формулы.

Уравнение динамики вращательного движения твердого тела относительно неподвижной оси (аналогично уравнению второго закона Ньютона):

          и    ,

где - момент инерции, ,  – угловое ускорение, рад/с², М – суммарный момент внешних сил.

Модуль угловой скорости: 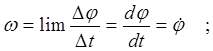   где - модуль угловой скорости, [] - рад/с.; - угол, на который поворачивается тело за промежуток времени ;  []- рад,

Модуль углового ускорения: 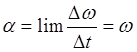, где  - угловое ускорение, рад/с²; - изменение угловой скорости за время ; [] - рад/с,

Момент инерции тела для диска: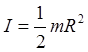, где  момент инерции, , -  масса диска, кг,   - радиус диска,м.

Модуль момента силы: ,  где l – плечо, [] – м, F– сила, действующая на тело;  [F] – н.

Число оборотов равно: 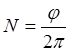, где N – число оборотов, φ – угол поворота, [] - рад.

3. Графический материал

4. Решение.

В основе данной расчетно-графической работы лежит вращательное движение стержня относительно неподвижной оси Z, которая проходит через центр диска. Запишем уравнение динамики вращательного движения:

.

Сумма проекций моментов внешних сил в данном случае равна разности, так как на тело действуют два момента силы, вызывающие вращение в противоположное направление, и  поэтому один из них условно принято считать положительным, а второй отрицательным:

.

где М_{z сопр} – момент сопротивления, по условию равный κ•ω² .

С другой стороны, угловое ускорение по определению равно:

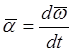, где  - угловая скорость.

Теперь уравнение вращательного движения можно записать в виде:

.

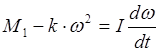 Так как , то умножим и разделим данное соотношение на : .

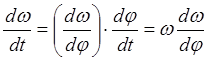Подставим  получившееся соотношение 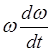 в уравнение:

 

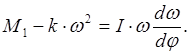
Разделим переменные в получившемся дифференциальном уравнении:

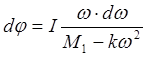
и проинтегрируем его:

 .

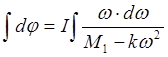Возьмем интеграл:

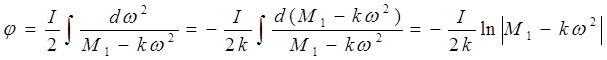                            .     (1)                              

Число оборотов равно:

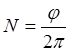                                        ,                                           (2)

где N – число оборотов, φ – угол поворота. Подставим  формулу (1) в  формулу (2):

.

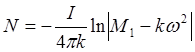Момент инерции для диска равен:

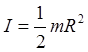,                                              (3)

где R – радиус диска, по условию равный 0,75 м. Подставив формулу (3) в формулу (2), окончательно имеем:

.

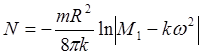Знак «минус» указывает на то, что проекции моментов сил выбраны в противоположных направлениях. Знак «минус» не влияет на конечный результат, поэтому при вычислении его можно не учитывать. Подставим в формулу числовые значения и вычислим:

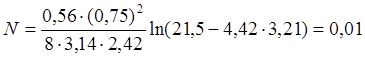
Вывод: диск сделает 0,01 оборота, до того, как его угловая скорость станет равной 3,21 рад/с. Таким образом, вращаясь с такой скоростью, диск не успевает сделать даже один оборот вокруг своей оси. Это говорит о том, что приложенная к нему сила достаточно велика по значению.