Электромагнитные колебания в простом колебательном контуре. Исследование зависимостей периода колебаний от индуктивности и ёмкости

возникает электрическое поле, энергия которого равна 1/2(q²/C)/ Если затем отключить источник напряжения и замкнуть конденсатор на индуктивность, ёмкость начнёт разряжаться и в контуре потечёт ток. В результате энергия электрического поля будет уменьшаться, но зато возникает все возрастающая энергия магнитного поля, обусловленного током, текущим через индуктивность.  Эта энергия равна 1/2LI². Поскольку активное сопротивление контура равно нулю, полная энергия, слагающаяся из энергий электрического и магнитного полей, не расходуется на нагревание проводов и будет оставаться постоянной. Поэтому в момент, когда напряжение на конденсаторе, а следовательно, и энергия электрического поля обращается в нуль, энергия магнитного поля,  а значит, и ток достигают наибольшего значения (стадия 2, начиная  с этого момента ток течет за счет э.д.с. самоиндукции). В дальнейшем ток уменьшается и, когда заряды на обкладках достигнут первоначального значения q, сила тока танет равной нулю (стадия 3). Затем те же процессы протекают в обратном направлении (стадия 4 и 5), после чего система приходит в исходное состояние (стадия 5) и весь цикл повторяется снова и снова. В ходе процесса периодически изменяются заряд на обкладках, напряжение на конденсаторе и сила тока, текущего через индуктивность. Колебания сопровождаются взаимными превращениями энергий электрического и магнитного полей.

Всякий реальный контур обладает активным сопротивлением. Энергия, запасенная в контуре, постепенно расходуется в этом сопротивлении на нагревание, вследствии чего свободные колебания затухают. При наличии в контуре активного сопротивления сила тока опережает по фазе  напряжение на конденсаторе более чем на . Затухание характеризуется логарифмическим декрементом затухания .

Колебательный контур также характеризуется его добротностью, величине, обратно пропорциональной логарифмическому декременту.

2)

3) Заряд на обкладках конденсатора изменется по гармоническому закону с частотой, определяемой выражением 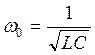. Эта частота называется собственной частотой контура. Для периода колебаний получается так называемая формула Томсона

В случае затухающих колебаний R¹0 , формула Томсона преобразуется в:

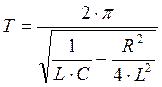
Затухание колебаний принято характеризовать логарифмическим декрементов затухания

,

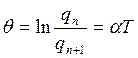здесь    - амплитуда соответствующей величины (q, U или I).

Логарифмический декремент затухания обратен числу колебаний Ne, совершаемых за время, в течении которого амплитуда уменьшается в е раз.

Добротность контура обратно пропорциональна логарифмическому декременту затуханий:                               .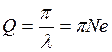  

Добротность контура тем выше, чем большее число колебаний успевает совершиться прежде, чем амплитуда уменьшится в е раз.

В случае слабого затухания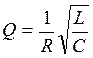                 

Схема установки:  

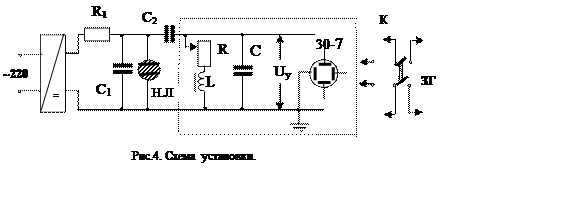L – катушка с сердечником

R1, R -  сопротивления

С, С1- конденсаторы

Н.Л. – неоновая лампа

Расчётные формулы:

   - формула для расчёта периода колебаний

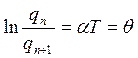        -формула для расчёта логарифмического декремента затухания

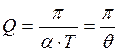  -формула для расчёта добротности

,где :

L – индуктивность катушки,   Гн

С – ёмкость конденсатора,   Ф

R – активное сопротивление,    Ом

  -отношение между двумя последующими амплитудами колебания

Q  - добротность

T – период  ,   с

Формулы погрешности:

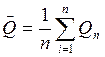 - расчёт среднего значения

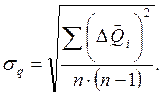  -среднеквадратичная погрешность

Таблицы измерений и вычислений:

Таблица 1.

Таблица 2.

Примеры расчётов:

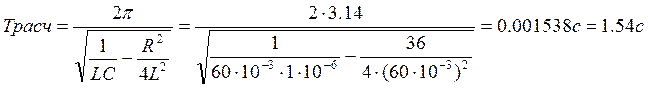
ln(q_n/q_n+1)=ln(12/8)=0.405

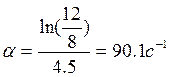
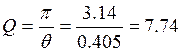
Расчёт погрешностей:

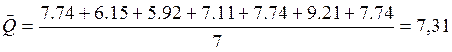
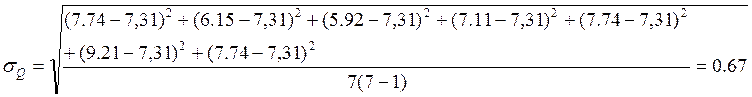
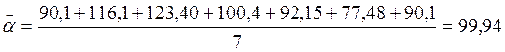
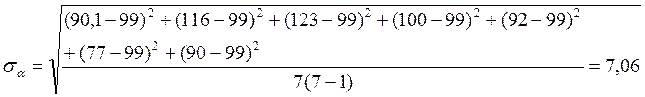
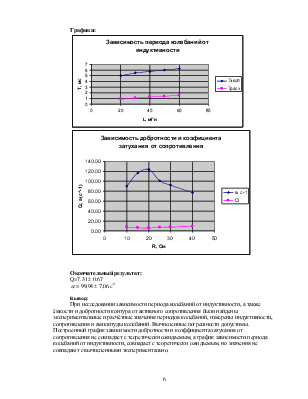
Графики:

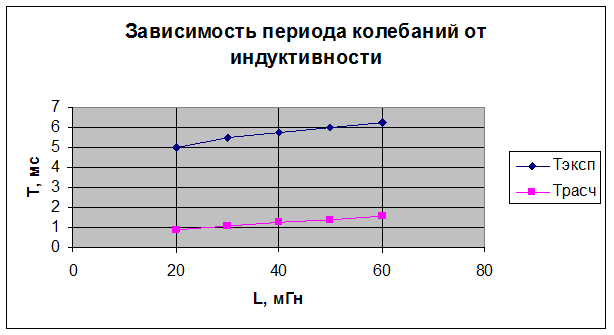
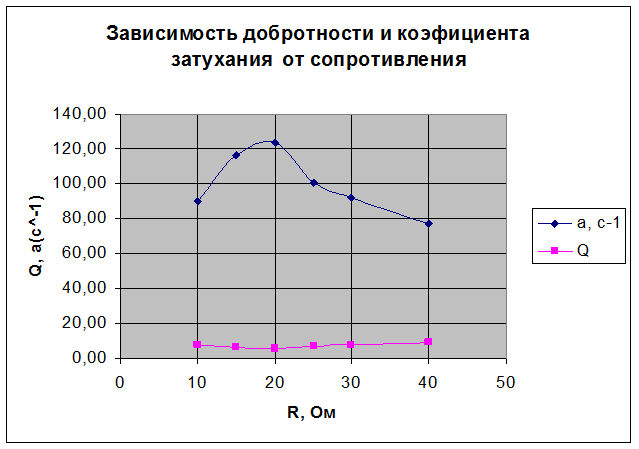
Окончательный результат:

            Q=7.310.67

            c^-1

Вывод:

            При исследовании зависимости периода колебаний от индуктивности, а также ёмкости и добротности контура от активного сопротивления были найдены экспериментальные и расчётные значения периодов колебаний, измерены индуктивности, сопротивления и амплитуды колебаний. Вычисленные погрешности допустимы. Построенный график зависимости добротности и коэффициента затухания от сопротивления не совпадает с теоретически ожидаемым, а график зависимости периода колебаний от индуктивности, совпадает с теоретически ожидаемым