Исследование эволюции кооперации методом теории игр. Исследование имитационной модели работы магазина. Исследование хаотической системы, страница 2

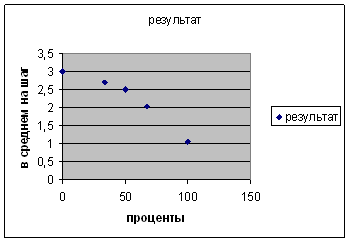
Рис. 2. График результатов различных вариантов действий при длительном взаимодействии фирм.

Ответ. При бесконечно долгом взаимодействии выгоднее сотрудничать, а не конфликтовать.

Выводы

1.  При однократном сотрудничестве лучше конфликтовать.

2.  При длительном взаимодействии лучше сотрудничать.

3.  Делать выбор в пользу самого простого алгоритма.

Лабораторная работа 2

«Исследование имитационной модели работы магазина»

Цель работы – исследование режимов работы магазина методом имитационного моделирования.

Общие сведения

Описываемый метод заключается в построении программы, имитирующей реальное функционирование моделируемой системы. Программная модель содержит очереди, пункты обслуживания, клиентов. При ее работе имитируется входной поток клиентов, а также прохождение клиентами всех фаз обслуживания.

Дано

Магазин «традиционного» типа, где вошедший покупатель выбирает товар, идет в кассу. Если в кассе имеется очередь, то он стоит в ней. После оплаты он переходит в отдел, где тоже может быть очередь. Получив товар, покупатель покидает магазин.

1 касса.

1 отдел.

Емкость магазина 20 человек.

Время работы магазина 480 мин.

Интенсивность входящих покупателей – 1человек в минуту.

Интенсивность выбора товар –  1человек в минуту.

Интенсивность обслуживания в кассе – 1 человек в минуту.

Интенсивность обслуживания в отделе – 1 человек в минуту.

Наиболее важный результат – число обслуженных покупателей.

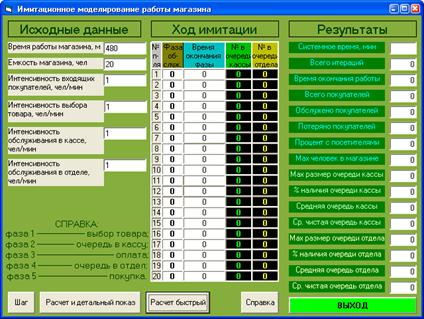
Рис. 3. Скриншот программы имитационного моделирования магазина.

Задача. Получить прибыль, обслужив не менее 95% входящих покупателей  с минимальными затратами.

Один из способов улучшения работы магазина это изменение таких параметров как интенсивность обслуживания в кассе и интенсивность обслуживания в отделе.

Решение.

Пусть интенсивность обслуживания в кассе будет 0,5; 1; 2 человека/мин. То есть в 2 раза меньше начального, начальное, в два раза больше начального условия.

Пусть интенсивность обслуживания в отделе также будет в 2 раза меньше начального, начальное и в два раза больше начального условия, 0,5; 1; 2.

Пусть длительность периода наблюдений составит 10 дней.

Все комбинации изменяемых величин, среднее количество обслуженных покупателей при каждой комбинации изменяемых величин, отклонение от средней величины, коэффициент Стьюдента для каждой комбинации и величина доверительного интервала, который по условию задачи составляет 95 %,  показаны в таблице 2.

                                                                                                                Табл. 2

касса	0,5	1	2	0,5	1	2	0,5	1	2
отдел	0,5	0,5	0,5	1	1	1	2	2	2
день1	255	259	246	263	467	457	250	471	451
день2	250	254	242	257	471	472	264	471	494
день3	245	266	274	247	470	463	265	484	474
день4	235	258	259	256	455	473	278	467	481
день5	244	255	246	251	457	470	243	468	472
день6	241	253	246	269	448	479	249	460	474
день7	246	253	252	251	476	479	263	466	513
день8	246	252	267	261	466	472	259	460	456
день9	251	266	275	268	461	479	243	475	470
день10	237	271	263	260	468	450	258	479	463
среднее	245	259	257	258	464	469,4	257	470	475
отклонение ежедневное	6,2	6,7	12,3	7,3	8,5	9,9	11,1	7,7	18,1
отклонение выборочного среднего	2,0	2,1	3,9	2,3	2,7	3,1	3,5	2,4	5,7
коэф Стьюдента	2,3	2,3	2,3	2,3	2,3	2,3	2,3	2,3	2,3
доверительный 95%	4,4	4,8	8,8	5,2	6,1	7,1	7,9	5,5	13,0