Интерполяция. Введение. Общая постановка задачи (Решение задач в среде программ Microsoft Excel или OpenOffice.org Calc)

Проведя аналогичные преобразования для Х=Х₃ и Х=Х₄, получим

 

Подставив (24) в (21), получим

 

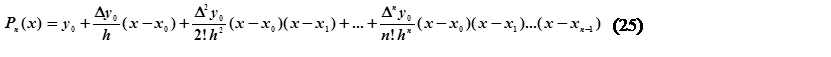На примере исходных данных, приведенной в таблице 2, рассмотрим методику вычислений значений интерполируемой функции для значений аргумента х, не совпадающих с узловыми точками таблицы. Вычислим значение функции Y для Х=1.

P₄(1)=0,696+1,579/0,4*(1-0,0)+(-2,685)*(1-0,0)*(1-0,4)/(2*0,4²) + 8,246*(1‑0,0)*(1-0,4)*(1-0,8)/(6*0,4³)+ (‑25,06)*(1‑0,0)*(1‑0,4)*(1‑0,8)*(1‑1,2)/(24*0,4⁴) = 3,1649

1.5.3. Организация ручных вычислений по первой формуле Ньютона

Рассмотрим пример выполнения ручных вычислений по первой формуле Ньютона.

Задана таблица значений функции, содержащая 4 узла:

Для данных этой таблицы вычислим таблицу конечных разностей

Вычислим значения коэффициентов полинома Ньютона

a₀=Y₀=2;
a₁= Δy₀/h= 2/1!/1=2;
a₂= Δ²Y₀/(2!h²)=1/(2!*1²) =0,5;
a₃= Δ³Y₀/(3!h³)=-5/6.

Используя вычисленные значения коэффициентов a₀ ,a₁ , a₂ , a₃ запишем формулу для полинома Ньютона:

P₃(x)=2+2(x-1)+0,5(x-1)(x-2)-5/6(x-1)(x-2)(x-3)=

=-5/6x³+5,5x²-26/3x+6

Эту формулу мы можем использовать для вычисления значений функции Y(x) в любой точке интервала от х=1 до х=4.

1.5.4. Реализация алгоритма интерполяции по первой формуле Ньютона в среде программы Microsoft Excel

1.  Введем в таблицу на листе Excel исходные данные, записанные в столбцах Х и Y(X) таблицы 2.

2.  По формулам (19), (20) и формулам, приведённым в таблице 1, сформируем таблицу 2 - таблицу конечных разностей до четвёртого уровня. Эти формулы, введенные в ячейки таблицы Excel, приведены на рис. 13.

 

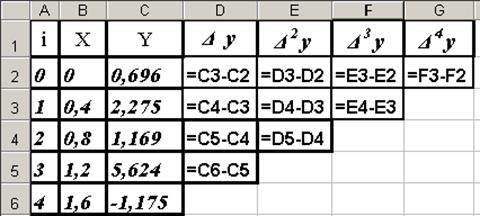Рис. 13. Формулы, использованные для вычисления значений конечных разностей функции Y(Х) в таблице 2

3.  В ячейку G6 для вычисления значения шагового приращения аргумента h введем формулу "=$В$3-$В$2".

4.  В ячейки строки 7 введём значения индекса i, определяющего индекс строки таблицы.

5.  В ячейках строки 8 вычислим степени hⁱ, а в ячейках строки девять запишем формулы для определения факториалов i!.

6.  На рис. 14 показаны формулы, используемые в таблице для вычисления значений коэффициентов a_i (i=0,1,2,3,4) для вычислительной формулы полинома Ньютона.

 

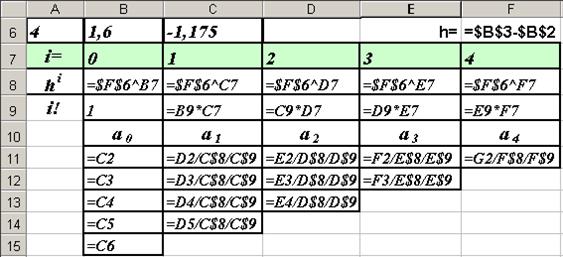Рис. 14. Формулы, введенные в ячейки листа Excel, для вычисления коэффициентов интерполирующего многочлена Ньютона

Для формирования этой таблицы достаточно ввести в ячейку В11 формулу "=С2" и протянуть её до ячейки В15 (формируется столбец ссылок на ячейки со значениями Y_i)

7.  На рис. 15 приведена таблица рис.14. в режиме отображения числовых значений, вычисленных по формулам рис. 14.

8.  Для выполнения вычислений значений интерполирующего полинома Ньютона в столбцах H, I и J сформируем разреженную таблицу. В столбец Н запишем номера строк таблицы от 0 до 8. В столбец I записываем значения аргумента Х от Х₀ = 0 до Х_k = 1,6.

9.  В ячейку J2 и введём формулу для вычисления значения интерполирующего полинома Ньютона:

=$B$11+(I2-$B$2)*$C$11+

(I2-$B$2)*(I2-$B$3)*$D$11+
(I2-$B$2)*(I2-$B$3)*(I2-$B$4)*$E$11+
(I2-$B$2)*(I2-$B$3)*(I2-$B$4)*(I2-$B$5)*$F$11

Здесь $B$11, $C$11, $D$11, $E$11, $F$11 - ссылки на коэффициенты a_i (i=0,1,2,3,4); I2 - ссылка на ячейку со значением аргумента x для точки, в которой вычисляется значение интерполирующего полинома Ньютона, $B$2, $B$3, $B$4, $B$5 - ссылки на ячейки, в которых записаны значения аргументов X_i (i=0,1,2,3,4).

Рис. 15. Результаты вычислений коэффициентов ai (i=0,1,2,3,4)  по формулам рис. 14

10.Протянув формулу, записанную в ячейку J2, по столбцу до ячейки J10, получим значения интерполирующего полинома для всех точек вектора Х. Результаты вычислений и график, построенный по таблице значений, показан на рис. 16.

 

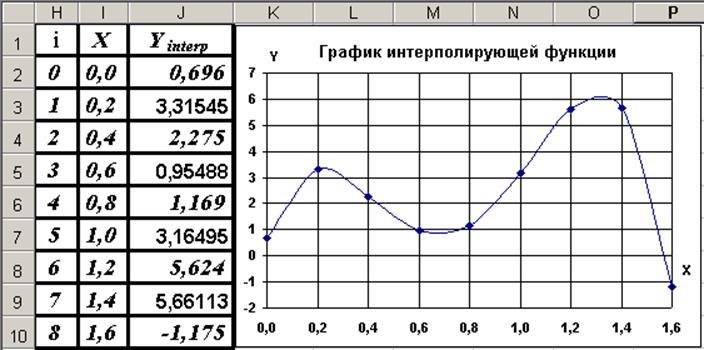Рис. 16. Таблица и график с результатами интерполяции

График, построенный по результатам интерполяции, сглажен. Для этого после выделения графика в окне "Формат ряда данных" на вкладке "Вид" включаем флажок "Сглаженная линия".Литература

1.  Мудров А.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. – Томск: МП “РАСКО”, 1991. – 272 с.: ил.

2.  Калиткин Н. Н. Численные методы. – М.: Наука, 1978. – 512 с.

3.  Любимов Е.Б. и др. Решение систем линейных алгебраических уравнений средствами программы Microsoft Excel. Методические указания. СПбГАСУ, - СПб., 2005. - 16 с.

4.  Заварыкин В.М. и др. Численные методы. - М.: Просвещение, 1990. -176 с.

Оглавление