Решение краевой задачи методом конечных разностей: Методические указания по выполнению лабораторной работы в курсе “Информатика”

ячейках от C3 до C8 вычисляем значения вспомогательной функции 1/(2 х_i+1), входящей взнаменатели функций p(x), q(x) и f(x). Вводим в C3 формулу "=1/(2*B3+1)" и протягиваем эту формулу до ячейкиC8;

5. 

В ячейки D3, E3 и F3 записываем формулы, соответствующие (13), для вычисления значений функций p(x), q(x) и f(x). Запись этих формул при вводе их в ячейки таблицы имеет следующий вид: "=-2*C3", "= ‑12*C3*C3" и "=(3*B3+1)*C3*C3" соответственно. При протягивании этих формул по столбцам D, Е и F до восьмой строки таблица заполняется так, как показано на рис. 2.

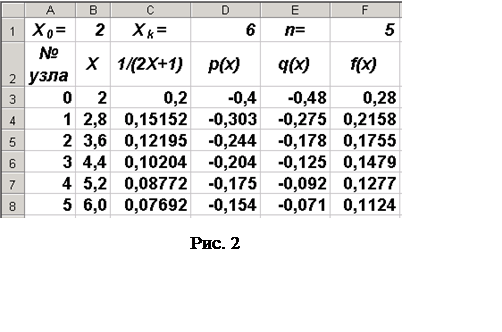6.  Далее начинаем заполнение столбцов G, H, I и J значениями коэффициентов A_i, C_i, B_i и F_i в соответствии с форматом системы уравнений (11). В ячейки G3, H3, I3 записываем значения, определяемые форматом первого уравнения системы (11): A₀=0, C₀=-1, В₀=0. В ячейку J3 записываем ссылку на ячейку J1, в которой записано начальное значение F₀=Y₀: "=J1".

7.  В ячейки G8, H8, I8 записываем значения, определяемые конечными условиями A₅=0, C₅=-1, В₅=0. В ячейку J8 записываем ссылку на ячейку L1, в которой записано начальное значение F_k= F₅ = Y_k :"=L1".

8. 

Далее заполняем столбцы G, H, I и J значениями коэффициентов A_i , C_i , B_i и F_i. В ячейку G4 вводим формулу "=1-D4*$H$1/2", соответствующую формуле

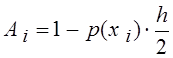для вычисления коэффициента A₁. После чего протягиваем эту формулу до ячейки G7.

9. 

Аналогично в ячейку Н4 вводим формулу для вычисления коэффициента С₁: "2-Е4*$H$1*$H$1", а в ячейку I4 вводим формулу для вычисления коэффициента B₁: "1+D4*$H$1/2", реализуя соответствующие формулы

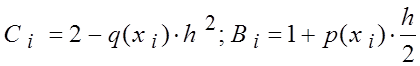Протягиваем эти формулы до ячеек Н7 иI7.

10. 

В ячейках столбца J формируем вектор правых частей системы уравнений (11). В ячейку J4 вводим формулу “=F4*$H$1*$H$1”, соответствующую формуле F_i = f_ih². Протягиваем эту формулу до ячейки J7. В результате получаем таблицу, показанную на рис. 3. Следует отметить, что в столбцах G, H, I и J этой таблицы записаны элементы матрицы, решаемой системы уравнений (11).

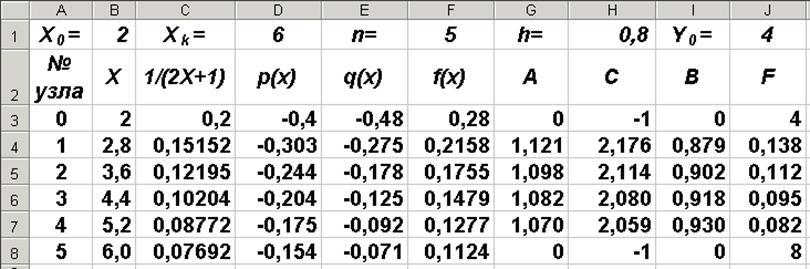Рис. 3

11.  Используя вычисленные значения коэффициентов A_i, C_i, B_i и F_i, находим в соответствии с формулами (18) и (19) значения коэффициентов a_i и b_i. В ячейку K3 запишем формулу для вычисления a₀ : "=I3/H3", а в ячейку L3 формулу для вычисления b₀.: "=-J3/H3". И далее в ячейки K4 и L4 вводим формулы, соответствующие (19), для вычисления коэффициентов 

 a₁ :"=I4/(H4-K3*G4)", и b₁: "=(G4*L3‑J4)/( H4‑K3*G4)".

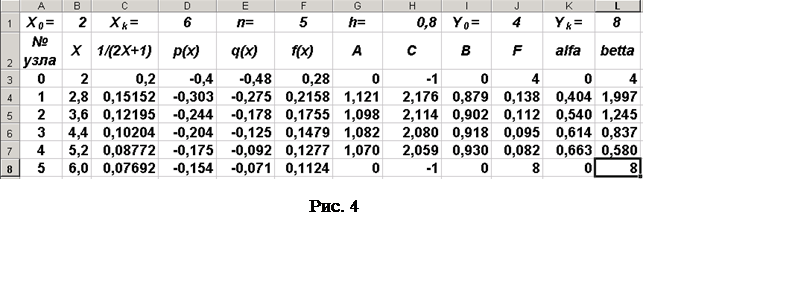
Протягиваем эти формулы до ячеек K8 и L8 соответственно. Результаты вычисления показаны на рис. 4.

12. 

Дальнейшие вычисления выполняются в столбце М по формулам обратного хода (21) и (22). В ячейку М8 введем формулу "=L8", представляющую ссылку на значение b_n. В ячейку М7 введем формулу "=L7+K7*M8", соответствующую и протянем ее до ячейки М3. Результаты вычислений показаны на рис. 5.

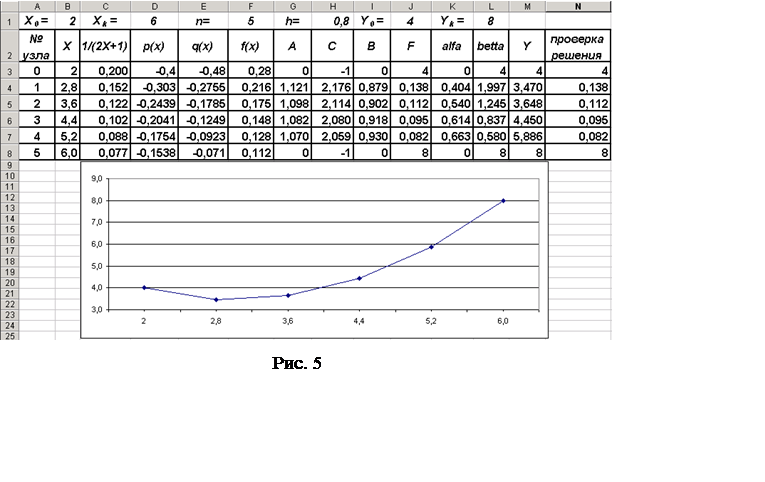
13.  Построим график функции Y(X), используя возможности мастера диаграмм программы MS Excel. Для этого выделим ячейки столбца значений функции Y(X) от ячейки М3 до М8 ивыполним процедуру создания диаграммы, используя средства "мастера диаграмм" программы MS Excel. Окончательный результат показан на рис. 5.

Проверка правильности полученного решения

Для проверки правильности полученного в столбце М решения Y(X) выполняется подстановкой полученного решения в уравнения исходной системы. В ячейки столбца N последовательно вводим формулы, реализующие вычислительный алгоритм, определяемый системой уравнений (11). В N3 введём формулу "=M3". Затемв N4 введём формулу  "=G4*M3‑H4*M4+I4*M5", реализующую левую часть уравнения (9). Эту формулу протягиваем до N8, получаясоответственно – "=G5*M4‑H5*M5+I5*M6" вN5, "=G6*M5-H6*M6+I6*M7" в N6,  "=G7*M6‑H7*M7+I7*M8" вN7 и "=G8*M7-H8*M8+I8*M9" вN8. Полученные в столбце N значения совпадают со значениями в столбце J, что позволяет судить о правильности полученного решения.

Варианты заданий для выполнения самостоятельной работы

Методом конечных разностей найти решение краевой задачи на сетке из 6 узлов.

Вариант 1

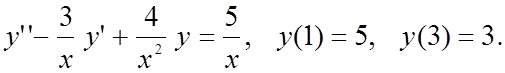Вариант 2

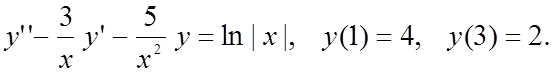Вариант 3

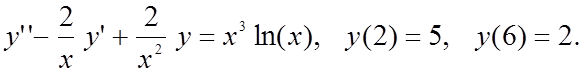Вариант 4

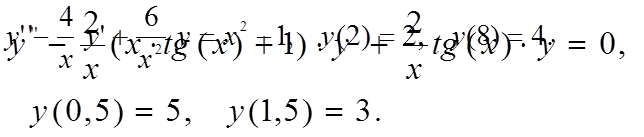Вариант 5

Вариант 6

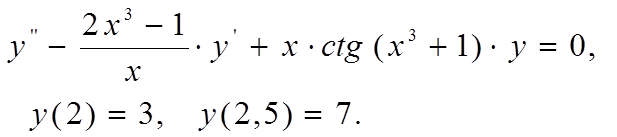Вариант 7

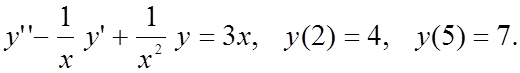Вариант 8

Вариант 9

Вариант 10

Вариант 11

Вариант 12

Вариант 13

Вариант 14

Вариант 15

Литература

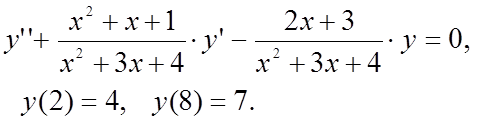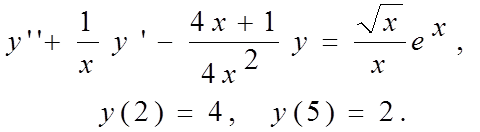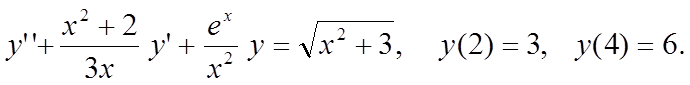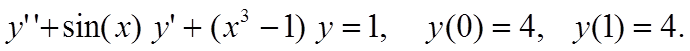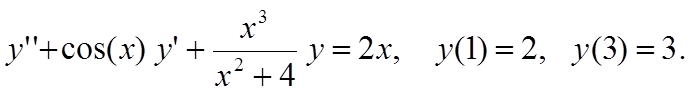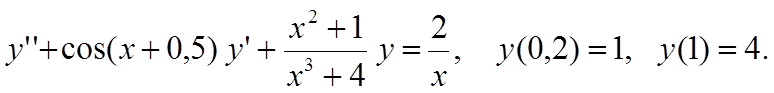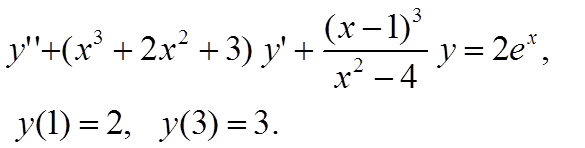1.  Пискунов Н.С. Дифференциальное и интегральное исчисления. М.:Физматгиз, 1963. – 856 с.

2.  Карпов В.В., Коробейников А.В. Математические модели задач строительного профиля и численные методы их исследования: Учеб. пособие. – СПб., СПбГАСУ, 1996. – 134 с.

3.  Бахвалов Н.С. Численные методы. – М.:Наука, 1973. – 632 с.

4.  Вагер Б.Г. Численные методы решения дифференциальных уравнений: Учеб. пособие – СПбГАСУ. – СПб. 2003. 114 с.

5.  Любимов Е.Б. и др. Решение систем линейных алгебраических уравнений средствами программы Microsoft Excel: Метод. указ. – СПб., СПбГАСУ, 2005. – 22 c.

СОДЕРЖАНИЕ

Основные понятия, используемые в постановках краевых задач. 3

Применение метода прогонки для решения систем линейных алгебраических уравнений с трёхдиагональными ленточными матрицами. 6

Реализация метода прогонки в среде программы MS Excel 6

Постановка задачи. 6

Проверка правильности полученного решения. 12

Варианты заданий для выполнения самостоятельной работы.. 13

Литература. 16