Бинарные деревья. Поиск узла с минимальным ключом. Вывод всех возможных путей в дереве, страница 6

private void PrintPaths (Node node)  // Print out all root-to-leaf paths

{

  ArrayList path = new ArrayList();

  PrintPaths (node, path, 0);

}

// Recursive helper. Параметр path уже содержит путь вплоть до текущего узла

private void PrintPaths (Node node, ArrayList path, int id)

{

  if (node == null)

    return;

  if (id < path.Count)

    path[id] = node.ManRef.ID; // Изменим элемент списка

  else

    path.Add (node.ManRef.ID); // Добавим элемент в список

  if (node.Left == null && node.Right == null) // Это—лист, пора выводить накопленный путь

  {

    foreach (int i in path)

      Console.Write (i.ToString() +  "  ");

    Console.WriteLine();

  }

  else // Otherwise try both subtrees

  {

    id++;

    PrintPaths (node.Left, path, id);

    PrintPaths (node.Right, path, id);

  }

}

Рассмотренный алгоритм посложнее предыдущих, поэтому рекомендую пройти его в режиме отладки. Заметьте, что индекс id, передаваемый в параметре имеет смысл текущего индекса в списке ArrayList, а не ключа в узле дерева. Вызовите метод PrintPaths с помощью такого кода.

Console.WriteLine ("\nPrinting all the paths:\n");

tree.PrintPaths();

Рассмотрим еще одну комбинаторную задачу, связанную со структурой бинарного дерева. Требуется вычислить количество различных деревьев, образованных из заданного количества узлов. Например, из одного узла можно составить одно дерево, из двух узлов можно составить два дерева.

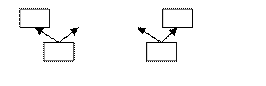
Из трех узлов можно составить пять топологически разных деревьев (деревьев с различной структурой).

Следующий метод решает поставленную задачу путем рекурсии. Алгоритм перебирает все узлы и вычисляет количество вариантов в предположении, что текущий узел стоит при корне. Если предположить, что слева от него расположено 0 узлов, то справа—все остальные, то есть (keys – 1). Если слева 1 узел, то справа—(keys – 2). В общую сумму вариантов вкладывается количество комбинаций расположений слева и справа. Здесь важно понять, что все новые комбинации можно получить из старых, а это—рекурсия.

public static int CountTrees (int keys)

{

  if (keys < 2) // Из одного (или нуля узлов) получим одно дерево

    return 1;

  int sum = 0; // Общая сумма

  for (int i=1; i <= keys; i++)

  {

    int

      left  = CountTrees (i - 1),

      right = CountTrees (keys - i);

    sum += left * right;

  }

  return sum;

}

Полезно мысленно просчитать (и тем самым проверить) работу алгоритма при keys = 3. Если слева от прикорневого узла стоит один узел, то справа тоже один. Если слева—два узла, то справа ноль, но два узла, стоящие слева, дают две комбинации. Осталось еще два варианта расположений узлов, возможных в случае, если слева от прикорневого узла пусто, а справа стоят два узла. Эти рассуждения получены из анализа рисунков, но без учета уже известного факта, что при keys = 2 имеются два дерева. Новые деревья получаются из старых добавлением одного узла.

Если сначала рассмотреть все способы добавки узла к первому дереву, то легко видеть, что их 3. Количество способов добавки узла ко второму дереву тоже три, но один из них повторяет уже сосчитанный вариант, поэтому имеем 3+2=5. Количество деревьев, образуемых из 4 узлов равно 14 и это число также образуется добавками одного узла к 5 старым расстановкам. Имеем (см. рисунок слева-направо) 4+3+2+3+2 = 14. Запустите метод и убедитесь, что из 16 узлов можно составить более 35 миллионов различных деревьев. Вызов метода можно осуществить так.

Console.WriteLine ("\nAll the different trees\n Nodes:\tTrees:");

for (int i=1; i<17; i++)

  Console.WriteLine ("  {0}\t {1}", i, Tree.CountTrees (i));

Как очистить буфер ввода в С++

void Clear (istream& is)

{            // В С и С++ это всегда было слабым местом

if (cin.eof()) // Подробности см. в MSDN

  return;

int n = is.rdbuf()->in_avail(); // Сколько байт в буфере?

while (n--)         // Выбираем все по одному

  is.rdbuf()->sbumpc();

is.clear();         // Снимаем признак ошибки в потоке ввода (failbit)

}